
【题目】已知二次函数f(x)=x2﹣ax+a(x∈R)同时满足:
①不等式f(x)≤0的解集有且只有一个元素;
②在定义域内存在0<x1<x2 , 使得不等式f(x1)>f(x2)成立.设数列{an}的前n项和Sn=f(n).
(1)求f(x)的表达式;
(2)求数列{an}的通项公式;
(3)设 ![]() ,cn=
,cn= ![]() ,{cn}的前n项和为Tn , 若Tn>2n+t对任意n∈N,n≥2恒成立,求实数t的取值范围.
,{cn}的前n项和为Tn , 若Tn>2n+t对任意n∈N,n≥2恒成立,求实数t的取值范围.
【答案】
(1)
解:由不等式f(x)≤0的解集有且只有一个元素得△=a2﹣4a=0,
解得a=0或a=4.
当a=0时,f(x)=x2在(0,+∞)上单调递增,故不存在0<x1<x2,使得不等式f(x1)>f(x2)成立;
当a=4时,f(x)=x2﹣4x+4在(0,2)上单调递减,故存在0<x1<x2,使得不等式f(x1)>f(x2)成立.
综上,f(x)=x2﹣4x+4
(2)
解:由(1)知: ![]() .
.
当n=1时,a1=S1=1.
当n≥2时,an=Sn﹣Sn﹣1=(n2﹣4n+4)﹣[(n﹣1)2﹣4(n﹣1)+4]=2n﹣5.
∴an= ![]()
(3)
解:∵ ![]() =
= ![]() ,∴b1=27,b2=9,
,∴b1=27,b2=9, ![]() ,
,
∴当n≥2时, ![]() =
= ![]() ,
,
∴当n≥2时, 
![]() ,
,
Tn>2n+t对n∈N,n≥2恒成立等价于t< ![]() 对n∈N,n≥2恒成立,
对n∈N,n≥2恒成立,
而 ![]() 是关于n的增函数,∴当n=2时,(Tn)min=16,
是关于n的增函数,∴当n=2时,(Tn)min=16,
∴实数t的取值范围是t<16
【解析】(1)由不等式f(x)≤0的解集有且只有一个元素得△=0,解得a=0或a=4.对a分类讨论,利用二次函数的单调性即可得出.(2)由(1)知: ![]() .当n=1时,a1=S1 . 当n≥2时,an=Sn﹣Sn﹣1 . 即可得出.(3)由(2)及其已知可得bn , cn , Tn , 再利用数列的单调性即可得出.
.当n=1时,a1=S1 . 当n≥2时,an=Sn﹣Sn﹣1 . 即可得出.(3)由(2)及其已知可得bn , cn , Tn , 再利用数列的单调性即可得出.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知向量 ![]() ,
, ![]() 满足|
满足| ![]() |=
|= ![]() ,|
,| ![]() |=1,且对任意实数x,不等式|
|=1,且对任意实数x,不等式| ![]() +x
+x ![]() |≥|
|≥| ![]() +
+ ![]() |恒成立,设
|恒成立,设 ![]() 与
与 ![]() 的夹角为θ,则tan2θ=( )
的夹角为θ,则tan2θ=( )
A.﹣ ![]()
B.![]()
C.﹣ ![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x),将f(x)图像沿x轴向右平移 ![]() 个单位,然后把所得到图像上每一点的纵坐标保持不变,横坐标扩大到原来的2倍,这样得到的曲线与y=2sin(x﹣
个单位,然后把所得到图像上每一点的纵坐标保持不变,横坐标扩大到原来的2倍,这样得到的曲线与y=2sin(x﹣ ![]() )的图像相同,那么y=f(x)的解析式为( )
)的图像相同,那么y=f(x)的解析式为( )
A.f(x)=2sin(2x﹣ ![]() )
)
B.f(x)=2sin(2x﹣ ![]() )
)
C.f(x)=2sin(2x+ ![]() )
)
D.f(x)=2sin(2x+ ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设 ![]() ,g(x)=ax+5﹣2a(a>0).
,g(x)=ax+5﹣2a(a>0).
(1)求f(x)在x∈[0,1]上的值域;
(2)若对于任意x1∈[0,1],总存在x0∈[0,1],使得g(x0)=f(x1)成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直线l⊥平面α,垂足为O,已知△ABC中,∠ABC为直角,AB=2,BC=1,该直角三角形做符合以下条件的自由运动:(1)A∈l,(2)B∈α.则C、O两点间的最大距离为 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分15分)如图,已知四棱锥P–ABCD,△PAD是以AD为斜边的等腰直角三角形,BC∥AD,CD⊥AD,PC=AD=2DC=2CB,E为PD的中点.

(Ⅰ)证明:CE∥平面PAB;
(Ⅱ)求直线CE与平面PBC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的几何体![]() 中,底面
中,底面![]() 为菱形,
为菱形, ![]() ,
, ![]() ,
, ![]() 与
与![]() 相交于
相交于![]() 点,四边形
点,四边形![]() 为直角梯形,
为直角梯形, ![]() ,
, ![]() ,
, ![]() ,平面
,平面![]() 底面
底面![]() .
.
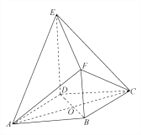
(1)证明:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com