
【题目】如图,四棱锥![]() ,底面
,底面![]() 侧面
侧面![]() ,
,![]() 分别为
分别为![]() 的中点,且
的中点,且![]() ,
,![]() ,
,![]() ,
,![]() .
.
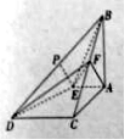
(I)证明:![]() 平面
平面![]() ;
;
(II)设![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
【答案】(I)证明见解析;(II)![]() .
.
【解析】
试题分析:(I)借助题设条件运用线面垂直的判定定理推证;(II)借助题设运用三棱锥的体积公式探求.
试题解析:
(I)证明:由题意知![]() 为等腰直角三角形,而
为等腰直角三角形,而![]() 为
为![]() 的中点,所以
的中点,所以![]() ,..........2分
,..........2分
又因为平面![]() 平面
平面![]() ,且
,且![]() ,所以
,所以![]() 平面
平面![]() ,................3分
,................3分
而![]() 平面
平面![]() ,所以
,所以![]() ,所以
,所以![]() 平面
平面![]() ,
,
连结![]() ,则
,则![]() ,
,![]() ,而
,而![]() ,
,![]() ,.......................5分
,.......................5分
所以![]() ,
,![]() ,
,![]() 是平行四边形,所以
是平行四边形,所以![]() ,
,![]() 平面
平面![]() ...........6分
...........6分
(II)因为![]() 平面
平面![]() ,即
,即![]() 平面
平面![]() ,
,![]() 是三棱锥
是三棱锥![]() 的高,........8分
的高,........8分
所以![]() ,..........................................10分
,..........................................10分
于是三棱锥![]() 的体积为
的体积为![]() ........12分
........12分


科目:高中数学 来源: 题型:
【题目】某高校大一新生中的6名同学打算参加学校组织的“雅荷文学社”、“青春风街舞社”、“羽乒协会”、“演讲团”、“吉他协会”五个社团,若每名同学必须参加且只能参加1个社团且每个社团至多两人参加,则这6个人中至多有1人参加“演讲团”的不同参加方法数为( )
A. 4680 B. 4770 C. 5040 D. 5200
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,可见部分如下:

试根据图表中的信息解答下列问题:
(1)求全班的学生人数及分数在[70,80)之间的频数;
(2)为快速了解学生的答题情况,老师按分层抽样的方法从位于[70,80),[80,90)和[90,100]分数段的试卷中抽取8份进行分析,再从中任选3人进行交流,求交流的学生中,成绩位于[70,80)分数段的人数X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() (
(![]() )的离心率为
)的离心率为![]() ,连接椭圆的四个顶点得到的四边形的面积为
,连接椭圆的四个顶点得到的四边形的面积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设椭圆![]() 的左焦点为
的左焦点为![]() ,右焦点为
,右焦点为![]() ,直线
,直线![]() 过点
过点![]() 且垂直于椭圆的长轴,动直线
且垂直于椭圆的长轴,动直线![]() 垂直
垂直![]() 于点
于点![]() ,线段
,线段![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,求点
,求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(3)设![]() 为坐标原点,取
为坐标原点,取![]() 上不同于
上不同于![]() 的点
的点![]() ,以
,以![]() 为直径作圆与
为直径作圆与![]() 相交另外一点
相交另外一点![]() ,求该圆面积的最小值时点
,求该圆面积的最小值时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经统计,某医院一个结算窗口每天排队结算的人数及相应的概率如下:
排除人数 | 0--5 | 6--10 | 11--15 | 16--20 | 21--25 | 25人以上 |
概率 | 0.1 | 0.15 | 0.25 | 0.25 | 0.2 | 0.05 |
(1)求每天超过20人排队结算的概率;
(2)求2天中,恰有1天出现超过20人排队结算的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com