
 гыAЁфnAn(n =1ЃЌ2ЃЌ3ЃЌЁ)НЛгкBnЃЌМЧаТЕФЧњБпЬнаЮAЁфnBnBn+1AЁфn+1ЃЌУцЛ§ЮЊbnЃЌЧѓ
гыAЁфnAn(n =1ЃЌ2ЃЌ3ЃЌЁ)НЛгкBnЃЌМЧаТЕФЧњБпЬнаЮAЁфnBnBn+1AЁфn+1ЃЌУцЛ§ЮЊbnЃЌЧѓ ЕФЧАnЯюКЭSnЃЛ
ЕФЧАnЯюКЭSnЃЛ ЁЃ
ЁЃ 
НтЃК(Ђё)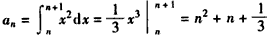 ЃЛ
ЃЛ
(Ђђ)вРЬтвтЃЌ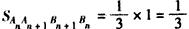 ЃЌ
ЃЌ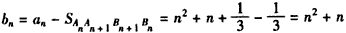 ЃЌ
ЃЌ
Ёр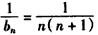 ЃЌ
ЃЌ
Ёр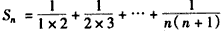
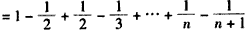 ЃЌ
ЃЌ
Ёр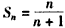 ЁЃ
ЁЃ
(Ђѓ)МЧжБНЧШ§НЧаЮCn+1An+1AnУцЛ§ЮЊdnЃЌ
дђ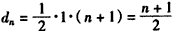 ЃЌ
ЃЌ
Ёр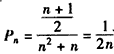 ЃЌ
ЃЌ
Ёр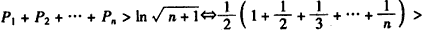
 ЃЌ
ЃЌ
дЪНМДжЄЃК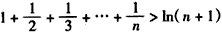 ЃЌ
ЃЌ
гУЪ§бЇЙщФЩЗЈжЄУїЃК
ЂйЕБn=1ЪБЃЌзѓБп=1ЃЌгвБп=lnaЃЌзѓБпЃОгвБпЃЌУќЬтГЩСЂЃЛ
ЂкМйЩшn=kЃЈkЁн1ЃЌkЁЪN*ЃЉЪБЃЌУќЬтГЩСЂЃЌ
МД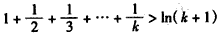 ЃЌ
ЃЌ
ЕБn=k+1ЪБЃЌ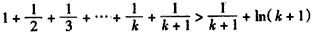 ЃЌ
ЃЌ
ЯТжЄЃК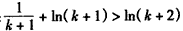
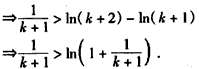
ЙЙдьКЏЪ§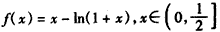 ЃЌ
ЃЌ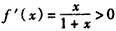 ЃЌЁрfЃЈxЃЉдк
ЃЌЁрfЃЈxЃЉдк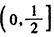 ЕЅЕїЕндіЃЌ
ЕЅЕїЕндіЃЌ
ЫљвдЕБ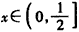 ЪБЃЌ
ЪБЃЌ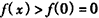 ЃЌЁрxЃОlnЃЈ1+xЃЉЃЌ
ЃЌЁрxЃОlnЃЈ1+xЃЉЃЌ
Ёп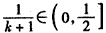 ЃЌ
ЃЌ
Ёр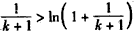 ЃЌ
ЃЌ
ЙЪУќЬтЖдn=k+1ЪБвВГЩСЂЃЌ
гЩЂйЂкЕУЃЌ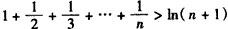 ЖдШЮвтnЁЪN*ЖМГЩСЂЃЌЙЪдУќЬтГЩСЂЁЃ
ЖдШЮвтnЁЪN*ЖМГЩСЂЃЌЙЪдУќЬтГЩСЂЁЃ


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com