
分析 取BC的中点N,连接AN交EF于点M,连接A′M,可证A′M⊥BM,由已知可得AM=MN=$\frac{\sqrt{3}a}{4}$=A′M,在Rt△MNB中,利用勾股定理可求MB,进而在Rt△A′MB中,利用勾股定理可求A′B的值.
解答 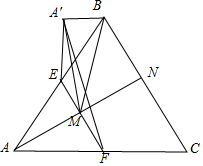 解:取BC的中点N,连接AN交EF于点M,连接A′M,
解:取BC的中点N,连接AN交EF于点M,连接A′M,
则A′M⊥EF.∵平面A′EF⊥平面BCFE,
∴A′M⊥平面BCFE,
∴A′M⊥BM,
∵AM=MN=$\frac{\sqrt{3}a}{4}$,
∴A′M=$\frac{\sqrt{3}a}{4}$,
在Rt△MNB中,MB=$\sqrt{M{N}^{2}+N{B}^{2}}$=$\sqrt{\frac{3{a}^{2}}{16}+\frac{{a}^{2}}{4}}$=$\frac{\sqrt{7}a}{4}$,
在Rt△A′MB中,A′B=$\sqrt{A′{M}^{2}+B{M}^{2}}$=$\sqrt{\frac{3{a}^{2}}{16}+\frac{7{a}^{2}}{16}}$=$\frac{\sqrt{10}a}{4}$.
故答案为:$\frac{\sqrt{10}a}{4}$.
点评 本题主要考查了直线与平面垂直的判断,考查了勾股定理在解三角形中的应用,考查了空间想象能力和推理论证能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若x>1,则x2>1”的否命题 | B. | 命题“若x>y,则x>|y|”的逆命题 | ||
| C. | 命题“若x=1,则x2+x-2=0”的否命题 | D. | 命题“若x2≥1,则x≥1”的逆否命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
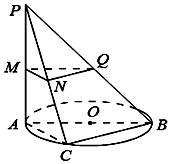 如图,⊙O在平面α内,AB是⊙O的直径,PA⊥平面α,C为圆周上不同于A、B的任意一点,M,N,Q分别是PA,PC,PB的中点.
如图,⊙O在平面α内,AB是⊙O的直径,PA⊥平面α,C为圆周上不同于A、B的任意一点,M,N,Q分别是PA,PC,PB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 夏威夷木瓜是木瓜类的名优品种,肉红微味甜深受市民喜爱.某果农选取一片山地种植夏威夷木瓜,收获时,该果农随机选取果树20株作为样本测量它们每一株的果实产量(单位:kg),获得的所有数据按照区间(40,45],(45,50],(50,55],(55,60]进行分组,得到频率分布直方图如图.已知样本中产量在区间(45,50]上的果树株数是产量在区间(50,60]上的果树株数的$\frac{4}{3}$倍.
夏威夷木瓜是木瓜类的名优品种,肉红微味甜深受市民喜爱.某果农选取一片山地种植夏威夷木瓜,收获时,该果农随机选取果树20株作为样本测量它们每一株的果实产量(单位:kg),获得的所有数据按照区间(40,45],(45,50],(50,55],(55,60]进行分组,得到频率分布直方图如图.已知样本中产量在区间(45,50]上的果树株数是产量在区间(50,60]上的果树株数的$\frac{4}{3}$倍.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com