已知等差数列{a
n}中,
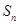
是它的前n项和.若S
16>0,且
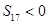
,则当
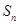
最大时n的值为( )
试题分析:由
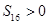
,
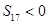
,故
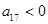
,且可得
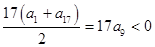
,则
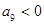
,所以等差数列是首项为正的递减数列.
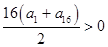
,
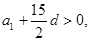
又
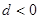
,故
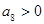
,所以等差数列的所有正数项和相加时
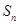
最大,故选A.
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
已知数列{
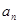
}、{
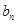
}满足:
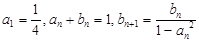
.
(1)求
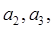
(2)证明:数列{
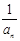
}为等差数列,并求数列
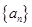
和{
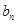
}的通项公式;
(3)设
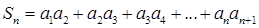
,求实数
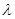
为何值时
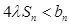
恒成立.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
各项均为正数的数列{a
n}中,设

,

,且
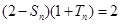
,

.
(1)设

,证明数列{b
n}是等比数列;
(2)设

,求集合

.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知数列
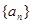
的前
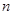
项和
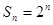
,数列
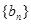
满足
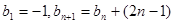
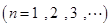
.
(1)求数列
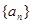
的通项
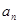
;
(2)求数列
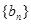
的通项
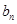
;
(3)若
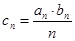
,求数列
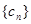
的前
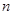
项和
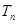
.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知首项为

的等比数列

不是递减数列,其前n项和为

,且

成等差数列。
(1)求数列

的通项公式;
(2)设

,求数列

的最大项的值与最小项的值。
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
等差数列

的前

项和为

,且

,则过 点

和

的直线的斜率是( )
| A.1 | B.2 | C.4 | D. |
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
在公差为d的等差数列{a
n}中,我们可以得到a
n=a
m+(n﹣m)d (m,n∈N
+).通过类比推理,在公比为q的等比数列{b
n}中,我们可得( )
| A.bn=bm+qn﹣m | B.bn=bm+qm﹣n |
| C.bn=bm×qm﹣n | D.bn=bm×qn﹣m |
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
已知数列{a
n}满足a
n+2=a
n+1+a
n,若a
1=1,a
5=8,则a
3=( )
| A.1 | B.2 | C.3 | D.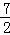 |
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
下列命题正确的是 ( )
①若数列
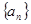
是等差数列,且
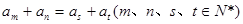
,
则
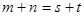
;
②若
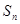
是等差数列
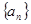
的前
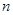
项的和,则
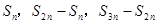
成等差数列;
③若
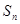
是等比数列
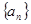
的前
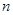
项的和,则
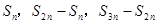
成等比数列;
④若
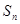
是等比数列
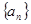
的前
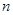
项的和,且
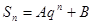
;(其中
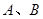
是非零常数,
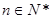
),则
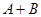
为零.
查看答案和解析>>

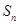 是它的前n项和.若S16>0,且
是它的前n项和.若S16>0,且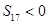 ,则当
,则当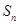 最大时n的值为( )
最大时n的值为( ) 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案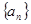 是等差数列,且
是等差数列,且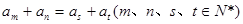 ,
,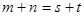 ;
;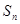 是等差数列
是等差数列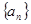 的前
的前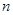 项的和,则
项的和,则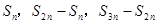 成等差数列;
成等差数列;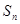 是等比数列
是等比数列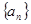 的前
的前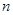 项的和,则
项的和,则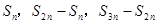 成等比数列;
成等比数列;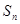 是等比数列
是等比数列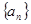 的前
的前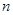 项的和,且
项的和,且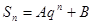 ;(其中
;(其中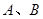 是非零常数,
是非零常数,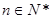 ),则
),则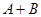 为零.
为零.