
给出以下三个命题,其中所有正确命题的序号为____.
①已知等差数列{ }的前二项和为
}的前二项和为 ,
, 为不共线向量,又
为不共线向量,又 ,
,
若 ,则S2012=1006.
,则S2012=1006.
② 是函数
是函数 的最小正周期为4"的充要条件;
的最小正周期为4"的充要条件;
③已知函数f (x)=|x2-2|,若f (a) =" f" (b),且0<a<b,则动点P(a,b)到直线4x+3y-15=0的距离的最小值为1;
①②③
【解析】
试题分析:①∵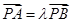 ,∴
,∴ ,∴
,∴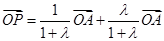 ,又
,又 ,∴
,∴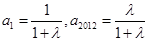 ,∴
,∴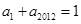 ,∴
,∴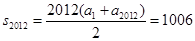 ,正确;②∵
,正确;②∵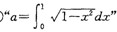 ,∴
,∴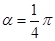 ,若函数
,若函数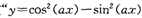
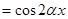 的最小正周期为4,则
的最小正周期为4,则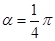 ,故
,故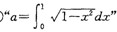 是函数
是函数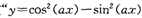 的最小正周期为4"的充要条件,正确;③∵函数f (x)=|x2-2|,若f (a) =" f" (b),且0<a<b,∴2-
的最小正周期为4"的充要条件,正确;③∵函数f (x)=|x2-2|,若f (a) =" f" (b),且0<a<b,∴2-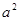 =
=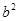 -2即
-2即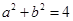 ,∴动点P(a,b)在以原点为圆心半径为2的圆上,又圆心(0,0)到直线4x+3y-15=0的距离为3,∴动点P(a,b)到直线4x+3y-15=0的距离的最小值为3-2=1,正确。
,∴动点P(a,b)在以原点为圆心半径为2的圆上,又圆心(0,0)到直线4x+3y-15=0的距离为3,∴动点P(a,b)到直线4x+3y-15=0的距离的最小值为3-2=1,正确。
考点:本题考查了共线向量基本定理、定积分的求法、三角函数的周期性及点到直线距离的综合运用
点评:此类问题综合性强,要求学生掌握相应的知识,一般可用特例法或者排除法求解。


科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com