
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 是边长为2的正方形,侧面
是边长为2的正方形,侧面![]() 底面
底面![]() ,
,![]() .
.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)当三棱锥![]() 体积最大时,求二面角
体积最大时,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)利用面面垂直的性质证得![]() ,利用线面垂直的性质证得
,利用线面垂直的性质证得![]() ,进而可得
,进而可得![]() 面
面![]() ,平面
,平面![]() 平面
平面![]() ;
;
(2)首先由不等式证得当![]() 时,三棱锥体积最大,然后建立空间直角坐标系,利用空间向量来求二面角的平面角,不难求解.
时,三棱锥体积最大,然后建立空间直角坐标系,利用空间向量来求二面角的平面角,不难求解.
(1)证明:∵侧面![]() 底面
底面![]() ,侧面
,侧面![]() 底面
底面![]() ,四边形
,四边形![]() 为正方形,∴
为正方形,∴![]() ,
,![]() 面
面![]() ,∴
,∴![]() 面
面![]() ,
,
又![]() 面
面![]() ,∴
,∴![]() ,
,![]() 平面
平面![]() ,
,![]() 面
面![]() ,∴
,∴![]() ,
,
![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() 面
面![]() ,
,![]() 面
面![]() ,
,
∴平面![]() 平面
平面![]() .
.
(2)![]() ,
,
求三棱锥![]() 体积的最大值,只需求
体积的最大值,只需求![]() 的最大值.
的最大值.
令![]() ,由(1)知,
,由(1)知,![]() ,∴
,∴![]() ,
,
而![]() ,当且仅当
,当且仅当![]() ,即
,即![]() 时,
时,![]() 的最大值为
的最大值为![]() .
.
如图所示,分别取线段![]() ,
,![]() 中点
中点![]() ,
,![]() ,连接
,连接![]() ,
,![]() ,以点
,以点![]() 为坐标原点,以
为坐标原点,以![]() ,
,![]() 和
和![]() 分别作为
分别作为![]() 轴,
轴,![]() 轴和
轴和![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() .
.
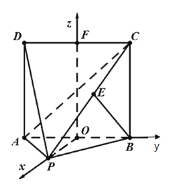
由已知![]() ,所以
,所以![]() ,
,
令![]() 为面
为面![]() 的一个法向量,则有
的一个法向量,则有![]() ,∴
,∴![]()
易知![]() 为面
为面![]() 的一个法向量,二面角
的一个法向量,二面角![]() 的平面角为
的平面角为![]() ,
,![]() 为锐角
为锐角
则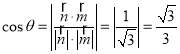 .
.


科目:高中数学 来源: 题型:
【题目】某超强台风登陆海南省.据统计,本次台风造成全省直接经济损失119.52亿元,适逢暑假,小明调查住在自己小区的50户居民由于台风造成的经济损失,作出如下频率分布直方图:
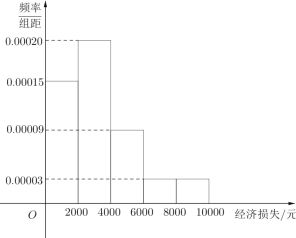
| 经济损失4000元以下 | 经济损失4000元以上 | 合计 |
捐款超过500元 | 30 | ||
捐款低于500元 | 6 | ||
合计 |
台风后区委会号召小区居民为台风重灾区捐款,小明调查的50户居民捐款情况如上表,在表格空白处填写正确数字,并说明是否有![]() 以上的把握认为捐款数额是否多于或少于500元和自身经济损失是否到4000元有关?
以上的把握认为捐款数额是否多于或少于500元和自身经济损失是否到4000元有关?
附:临界值表
| 2.072 | 2.706 | 3.841 | 5.024 | 6635 | 7.879 | 10.828 |
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
参考公式: ![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经销商第一年购买某工厂商品的单价为![]() (单位:元),在下一年购买时,购买单价与其上年度销售额(单位:万元)相联系,销售额越多,得到的优惠力度越大,具体情况如下表:
(单位:元),在下一年购买时,购买单价与其上年度销售额(单位:万元)相联系,销售额越多,得到的优惠力度越大,具体情况如下表:
上一年度 销售额/万元 |
|
|
|
|
|
|
商品单价/元 |
|
|
|
|
|
|
为了研究该商品购买单价的情况,为此调查并整理了![]() 个经销商一年的销售额,得到下面的柱状图.
个经销商一年的销售额,得到下面的柱状图.
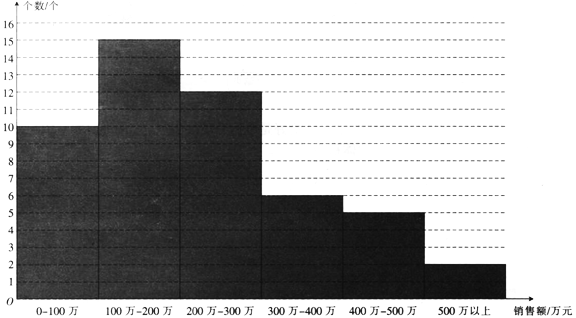
已知某经销商下一年购买该商品的单价为![]() (单位:元),且以经销商在各段销售额的频率作为概率.
(单位:元),且以经销商在各段销售额的频率作为概率.
(1)求![]() 的平均估计值.
的平均估计值.
(2)为了鼓励经销商提高销售额,计划确定一个合理的年度销售额![]() (单位:万元),年销售额超过
(单位:万元),年销售额超过![]() 的可以获得红包奖励,该工厂希望使
的可以获得红包奖励,该工厂希望使![]() 的经销商获得红包,估计
的经销商获得红包,估计![]() 的值,并说明理由.
的值,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC—A1B1C1中,BC=3,AB=4,AC=CC1=5,M,N分别是A1B,B1C1的中点.
(1)求证:MN//平面ACC1A1;
(2)求点N到平面MBC的距离.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家具厂生产一种办公桌,每张办公桌的成本为100元,出厂单价为160元,该厂为鼓励销售商多订购,决定一次订购量超过100张时,每超过一张,这批订购的全部办公桌出厂单价降低1元.根据市场调查,销售商一次订购量不会超过160张.
(1)设一次订购量为![]() 张,办公桌的实际出厂单价为
张,办公桌的实际出厂单价为![]() 元,求
元,求![]() 关于
关于![]() 的函数关系式
的函数关系式![]() ;
;
(2)当一次性订购量![]() 为多少时,该家具厂这次销售办公桌所获得的利润
为多少时,该家具厂这次销售办公桌所获得的利润![]() 最大?其最大利润是多少元?(该家具厂出售一张办公桌的利润=实际出厂单价-成本)
最大?其最大利润是多少元?(该家具厂出售一张办公桌的利润=实际出厂单价-成本)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)="xln" x–ax2+(2a–1)x,a![]() R.
R.
(Ⅰ)令g(x)=f'(x),求g(x)的单调区间;
(Ⅱ)已知f(x)在x=1处取得极大值.求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)=ax2+bx+c的图象与x轴有两个不同的交点,若f(c)=0且0<x<c时,f(x)>0,
(1)证明:![]() 是f(x)=0的一个根;
是f(x)=0的一个根;
(2)试比较![]() 与c的大小;
与c的大小;
(3)证明:-2<b<-1.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com