
【题目】已知等比数列{an}的各项均为正数,且a1a100+a3a98=8,则log2a1+log2a2+…+log2a100=( )
A.10
B.50
C.100
D.1000
【答案】C
【解析】解:∵数列{an}为各项均为正数的等比数列,且a1a100+a3a98=8,
∴a1a100=a2a99=a3a98=…=a50a51=4,
∴log2a1a100=log24=2,
即log2a1+log2a100=log2a2+log2a99=…=log2a50+log2a51=2,
∴log2a1+log2a2+…+log2a100
=(log2a1+log2a100)+(log2a2+log2a99)+…+(log2a50+log2a51)=2×50=100.
故选:C.
【考点精析】掌握数列的前n项和是解答本题的根本,需要知道数列{an}的前n项和sn与通项an的关系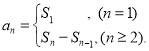 .
.


科目:高中数学 来源: 题型:
【题目】由于渤海海域水污染严重,为了获得第一手的水文资料,潜水员需要潜入水深为60米的水底进行作业,根据经验,潜水员下潜的平均速度为![]() (米/单位时间),每单位时间消耗氧气
(米/单位时间),每单位时间消耗氧气![]() (升),在水底作业10个单位时间,每单位时间消耗氧气
(升),在水底作业10个单位时间,每单位时间消耗氧气![]() (升),返回水面的平均速度为
(升),返回水面的平均速度为![]() (米/单位时间),每单位时间消耗氧气
(米/单位时间),每单位时间消耗氧气![]() (升),记该潜水员完成此次任务的消耗氧气总量为
(升),记该潜水员完成此次任务的消耗氧气总量为![]() (升).
(升).
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)若![]() ,求当下潜速度
,求当下潜速度![]() 取什么值时,消耗氧气的总量最少.
取什么值时,消耗氧气的总量最少.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念,记交通指数为![]() ,其范围为
,其范围为![]() ,分为五个级别,
,分为五个级别, ![]() 畅通;
畅通; ![]() 基本畅通;
基本畅通; ![]() 轻度拥堵;
轻度拥堵; ![]() 中度拥堵;
中度拥堵; ![]() 严重拥堵.早高峰时段(
严重拥堵.早高峰时段(![]() ),从某市交通指挥中心随机选取了三环以内的50个交通路段,依据其交通指数数据绘制的频率分布直方图如图.
),从某市交通指挥中心随机选取了三环以内的50个交通路段,依据其交通指数数据绘制的频率分布直方图如图.

(1)这50个路段为中度拥堵的有多少个?
(2)据此估计,早高峰三环以内的三个路段至少有一个是严重拥堵的概率是多少?
(3)某人上班路上所用时间若畅通时为20分钟,基本畅通为30分钟,轻度拥堵为36分钟,中度拥堵为42分钟,严重拥堵为60分钟,求此人所用时间的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆![]() 过定点
过定点![]() 且与圆
且与圆![]() 相切,记动圆圆心
相切,记动圆圆心![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)过点![]() 且斜率不为零的直线交曲线
且斜率不为零的直线交曲线![]() 于
于![]() ,
, ![]() 两点,在
两点,在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得直线
,使得直线![]() 的斜率之积为非零常数?若存在,求出定点的坐标;若不存在,请说明理由.
的斜率之积为非零常数?若存在,求出定点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
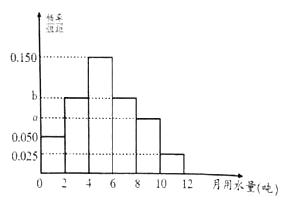
【题目】某市为了鼓励市民节约用水,实行“阶梯式”水价,将该市每户居民的月用水量划分为三档:月用水量不超过4吨的部分按2元/吨收费,超过4吨但不超过8吨的部分按4元/吨收费,超过8吨的部分按8元/吨收费.
(1)求居民月用水量费用![]() (单位:元)关于月用电量
(单位:元)关于月用电量![]() (单位:吨)的函数解析式;
(单位:吨)的函数解析式;
(2)为了了解居民的用水情况,通过抽样,获得今年3月份100户居民每户的用水量,统计分析后得到如图所示的频率分布直方图,若这100户居民中,今年3月份用水费用不超过16元的占60%,求![]() 的值;
的值;
(3)若地区居民用水量平均值超过6吨,则说明该地区居民用水没有节约意识在满足(2)的条件下,请你估计![]() 市居民用水是否有节约意识(同一组中的数据用该组区间的中点值作代表).
市居民用水是否有节约意识(同一组中的数据用该组区间的中点值作代表).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(文科)某出租车公司响应国家节能减排的号召,已陆续购买了140辆纯电动汽车作为运营车辆,目前我国主流纯电动汽车按续驶里程数![]() (单位:公里)分为3类,即
(单位:公里)分为3类,即![]() ,
, ![]() ,
, ![]() .对这140辆车的行驶总里程进行统计,结果如下表:
.对这140辆车的行驶总里程进行统计,结果如下表:

(1)从这140辆汽车中任取1辆,求该车行驶总里程超过5万公里的概率; (2)公司为了了解这些车的工作状况,决定抽取14辆车进行车况分析,按表中描述的六种情况进行分层抽样,设从![]() 类车中抽取了
类车中抽取了![]() 辆车. (ⅰ)求
辆车. (ⅰ)求![]() 的值; (ⅱ)如果从这
的值; (ⅱ)如果从这![]() 辆车中随机选取2辆车,求恰有1辆车行驶总里程超过5万公里的概率.
辆车中随机选取2辆车,求恰有1辆车行驶总里程超过5万公里的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() .
.
(1)求证:f(x)+f(1﹣x)= ![]() ;
;
(2)设数列{an}满足an=f(0)+f( ![]() )+f(
)+f( ![]() )+…+f(
)+…+f( ![]() )+f(1),求an;
)+f(1),求an;
(3)设数列{an}的前项n和为Sn , 若Sn≥λan(n∈N*)恒成立,求实数λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为[40,50],[50,60],…,[80,90],[90,100] 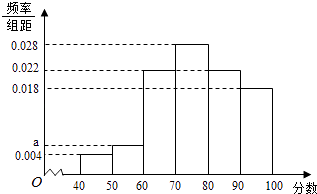
(1)求频率分布图中a的值;
(2)估计该企业的职工对该部门评分不低于80的概率;
(3)从评分在[40,60]的受访职工中,随机抽取2人,求此2人评分都在[40,50]的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com