
【题目】将边长为1的正方形![]() 沿对角线
沿对角线![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() ,在折起后形成的三棱锥
,在折起后形成的三棱锥![]() 中,给出下列三种说法:
中,给出下列三种说法:
①![]() 是等边三角形;②
是等边三角形;②![]() ;③三棱锥
;③三棱锥![]() 的体积是
的体积是![]() .
.
其中正确的序号是__________(写出所有正确说法的序号).
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前n项和为Sn , 公差d≠0,且S3+S5=50,a1 , a4 , a13成等比数列. (Ⅰ)求数列{an}的通项公式;
(Ⅱ)设 ![]() 是首项为1,公比为3的等比数列,求数列{bn}的前n项和Tn .
是首项为1,公比为3的等比数列,求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:若对定义域内任意x,都有![]() (a为正常数),则称函数
(a为正常数),则称函数![]() 为“a距”增函数.
为“a距”增函数.
(1)若![]() ,
,![]() (0,
(0,![]() ),试判断
),试判断![]() 是否为“1距”增函数,并说明理由;
是否为“1距”增函数,并说明理由;
(2)若![]() ,
,![]() R是“a距”增函数,求a的取值范围;
R是“a距”增函数,求a的取值范围;
(3)若![]() ,
,![]() (﹣1,
(﹣1,![]() ),其中k
),其中k![]() R,且为“2距”增函数,求
R,且为“2距”增函数,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)= ![]() x3﹣(1+a)x2+4ax+24a,其中常数a>1
x3﹣(1+a)x2+4ax+24a,其中常数a>1
(1)讨论f(x)的单调性;
(2)若当x≥0时,f(x)>0恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确命题的个数是( )
(1)cosα≠0是 ![]() 的充分必要条件
的充分必要条件
(2)f(x)=|sinx|+|cosx|,则f(x)最小正周期是π
(3)若将一组样本数据中的每个数据都加上同一个常数后,则样本的方差不变
(4)设随机变量ζ服从正态分布N(0,1),若P(ζ>1)=p,则 ![]() .
.
A.4
B.3
C.2
D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 的定义域为
的定义域为![]() ,若存在闭区间
,若存在闭区间![]() ,使得函数
,使得函数![]() 满足:①
满足:①![]() 在
在![]() 上是单调函数;②
上是单调函数;②![]() 在
在![]() 上的值域是
上的值域是![]() ,则称区间
,则称区间![]() 是函数
是函数![]() 的“和谐区间”.下列结论错误的是( )
的“和谐区间”.下列结论错误的是( )
A. 函数![]() 存在“和谐区间”
存在“和谐区间”
B. 函数![]() 不存在“和谐区间”
不存在“和谐区间”
C. 函数![]() 存在“和谐区间”
存在“和谐区间”
D. 函数![]() (
(![]() 且
且![]() )不存在“和谐区间”
)不存在“和谐区间”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥P﹣ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点. (I)证明:AE⊥PD;
(II)H是PD上的动点,EH与平面PAD所成的最大角为45°,求二面角E﹣AF﹣C的正切值.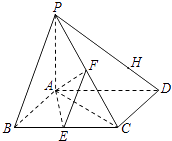
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数,f(x)=|x﹣a|
(Ⅰ)当a=2,解不等式,f(x)≥5﹣|x﹣1|;
(Ⅱ)若f(x)≤1的解集为[0,2],![]() +
+![]() =a(m>0,n>0),求证:m+2n≥4.
=a(m>0,n>0),求证:m+2n≥4.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com