
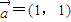 ,令
,令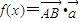 .
. ;
;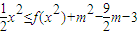 都恒成立,求实数m的取值范围.
都恒成立,求实数m的取值范围. ,再由向量数量积的坐标运算法则得f(x)的解析式,求导后可得f'(1),从而可得函数y=f(x)的表达式
,再由向量数量积的坐标运算法则得f(x)的解析式,求导后可得f'(1),从而可得函数y=f(x)的表达式 ,利用导数只需证明函数g(x)在(0,+∞)的下界大于零即可
,利用导数只需证明函数g(x)在(0,+∞)的下界大于零即可 x∈[-1,1]时恒成立,下面只需求函数
x∈[-1,1]时恒成立,下面只需求函数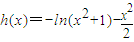 的最大值即可,利用导数可求这个值,再解不等式即可求实数m的取值范围
的最大值即可,利用导数可求这个值,再解不等式即可求实数m的取值范围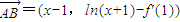
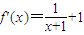 ,∴
,∴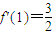 ∴
∴
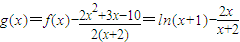 ∴
∴
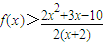
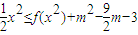 得
得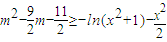
 ,∴
,∴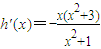 ∴当x∈[-1,0]时,h'(x)>0,h(x)为递增;
∴当x∈[-1,0]时,h'(x)>0,h(x)为递增; ,解得m≤-1或
,解得m≤-1或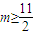
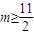


科目:高中数学 来源: 题型:
| a |
| AB |
| a |
| 2x2+3x-10 |
| 2(x+2) |
| 1 |
| 2 |
| 9 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)当b>0时,若对任意x∈R都有f(x)≤1,证明a≤2![]() ;
;
(2)当b>1时,证明对任意x∈[0,1],|f(x)|≤1的充要条件是b-1≤a≤2![]() ;?
;?
(3)当0<b≤1时,讨论:对任意x∈[0,1],|f(x)|≤1的充要条件.?
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)证明xn+2-xn是常数,并求数列{xn}的通项公式.
(2)若l的方程为y=![]() ,试问在△AnBnAn+1(n∈N*)中是否存在直角三角形?若存在,求出a的值;若不存在,请说明理由.
,试问在△AnBnAn+1(n∈N*)中是否存在直角三角形?若存在,求出a的值;若不存在,请说明理由.
(文)已知函数f(x)=![]() ax3
ax3![]() x2+cx+d(a、c、d∈R)满足f(0)=0,f′(1)=0,且f′(x)≥0在R上恒成立.
x2+cx+d(a、c、d∈R)满足f(0)=0,f′(1)=0,且f′(x)≥0在R上恒成立.
(1)求a、c、d的值.
(2)若h(x)=![]() x2-bx+
x2-bx+![]() ,解不等式f′(x)+h(x)<0.
,解不等式f′(x)+h(x)<0.
(3)是否存在实数m,使函数g(x)=f′(x)-mx在区间[m,m+2]上有最小值-5?若存在,请求出实数m的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com