
 .甲方每年受乙方生产影响的经济损失金额y=0.002t2(元),且乙方每生产一吨产品必须赔付甲方s元(以下s为赔付价格).
.甲方每年受乙方生产影响的经济损失金额y=0.002t2(元),且乙方每生产一吨产品必须赔付甲方s元(以下s为赔付价格). -st.
-st.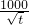 -s=
-s=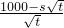 ,
,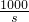 )2.
)2.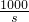 )2(吨);
)2(吨);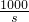 )2(吨);
)2(吨);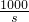 )2代入上式,得到甲方净收入v与赔付价格s之间的函数关系式v=
)2代入上式,得到甲方净收入v与赔付价格s之间的函数关系式v=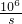 -
-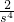 ×109.
×109.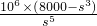 ,
, -st.利用导数法易求出乙方取得最大年利润的年产量,从而得出乙方获得最大利润时的年产t(吨)与赔付价格s(元)满足的关系式;
-st.利用导数法易求出乙方取得最大年利润的年产量,从而得出乙方获得最大利润时的年产t(吨)与赔付价格s(元)满足的关系式; .可以得到甲方净收入v与赔付价格s之间的函数关系式,利用导数法,求出答案.
.可以得到甲方净收入v与赔付价格s之间的函数关系式,利用导数法,求出答案.

 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:高中数学 来源: 题型:
| t |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com