
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为正方形,
为正方形, ![]() ,
, ![]() .
.

(Ⅰ)若![]() 是
是![]() 的中点,求证:
的中点,求证: ![]() 平面
平面![]() ;
;
(Ⅱ)若![]() ,
, ![]() ,求三棱锥
,求三棱锥![]() 的高.
的高.
【答案】(I)证明见解析;(II)![]() .
.
【解析】试题分析:(Ⅰ)连接![]() 交
交![]() 于
于![]() ,连接
,连接![]() .在三角形
.在三角形![]() 中,中位线
中,中位线 ![]() ,且
,且![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ;(Ⅱ)由
;(Ⅱ)由![]() ,
, ![]() 可得
可得![]() 与底面垂直,在
与底面垂直,在![]() 中,设
中,设![]() 的中点为
的中点为![]() ,连接
,连接![]() ,则
,则![]() 是三棱柱
是三棱柱![]() 的高,计算出三角形
的高,计算出三角形![]() 与
与![]() 面积,利用
面积,利用![]() 可求得点
可求得点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.
试题解析:
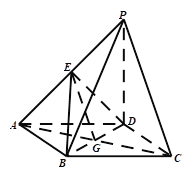
(Ⅰ)连接![]() 交
交![]() 于
于![]() ,连接
,连接![]() .在三角形
.在三角形![]() 中,
中,
中位线 ![]() ,
,
且![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(Ⅱ)在![]() 中,设
中,设![]() 的中点为
的中点为![]() ,连接
,连接![]() ,则
,则![]() ,又
,又![]() ,
,
∴![]() ,又∵
,又∵![]() ,
,
∴![]() ,∴
,∴ ![]() ,解得
,解得![]() .
.
所以点![]() 到平面
到平面![]() 的距离为:
的距离为: ![]() .
.
【方法点晴】本题主要考查线面平行的判定定理、利用等积变换求三棱锥的高,属于中档题.证明线面平行的常用方法:①利用线面平行的判定定理,使用这个定理的关键是设法在平面内找到一条与已知直线平行的直线,可利用几何体的特征,合理利用中位线定理、线面平行的性质或者构造平行四边形、寻找比例式证明两直线平行.②利用面面平行的性质,即两平面平行,在其中一平面内的直线平行于另一平面. 本题(1)是就是利用方法①证明的.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:高中数学 来源: 题型:
【题目】把函数y=cos2x+1的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),然后向左平移1个单位长度,再向下平移1个单位长度,得到的图象是( )
A.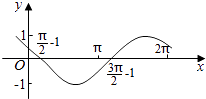
B.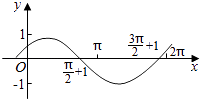
C.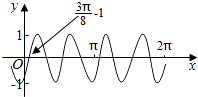
D.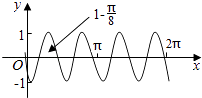
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)对任意x,y∈R,总有f(x)+f(y)=f(x+y),且当x>0时,f(x)<0,f(1)=-![]() .
.
(1)求证:f(x)是R上的单调减函数.
(2)求f(x)在[-3,3]上的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区有小学150所,中学75所,大学25所.先采用分层抽样的方法从这些学校中抽取30所学校对学生进行视力调查,应从小学中抽取 18 所学校,中学中抽取所学校.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(2x+ ![]() )+sin(2x﹣
)+sin(2x﹣ ![]() )+2cos2x﹣1,x∈R.
)+2cos2x﹣1,x∈R.
(1)求函数f(x)的最小正周期;
(2)求函数f(x)在区间[ ![]() ]上的最大值和最小值.
]上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的方程是
的方程是![]() (
(![]() ,
,![]() ).
).
(1)当![]() ,
,![]() 时,求曲线
时,求曲线![]() 围成的区域的面积;
围成的区域的面积;
(2)若直线![]() :
:![]() 与曲线
与曲线![]() 交于
交于![]() 轴上方的两点
轴上方的两点![]() ,
,![]() ,且
,且![]() ,求点
,求点![]() 到直线
到直线![]() 距离的最小值.
距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() 为奇函数.
为奇函数.
(1)求b的值;
(2)证明:函数f(x)在区间(1,+∞)上是减函数;
(3)解关于x的不等式f(1+x2)+f(-x2+2x-4)>0.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com