
【题目】设集合![]() ,设集合
,设集合![]() 是集合
是集合![]() 的非空子集,
的非空子集,![]() 中的最大元素和最小元素之差称为集合
中的最大元素和最小元素之差称为集合![]() 的直径. 那么集合
的直径. 那么集合![]() 所有直径为
所有直径为![]() 的子集的元素个数之和为( )
的子集的元素个数之和为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
先考虑最小元素为1,最大元素为72的情况:![]() 只有1种情况;
只有1种情况;![]() 且
且![]() ,共有
,共有![]() 种情况;
种情况;![]() 且
且![]() ,共有种
,共有种![]() 情况;以此类推……
情况;以此类推……![]() ,有1(
,有1(![]() )种情况.所以,此类满足要求的子集元素个数之和
)种情况.所以,此类满足要求的子集元素个数之和![]() ,计算可得:
,计算可得:![]() .再思考可以分为
.再思考可以分为![]() 等1949类,问题可得解.
等1949类,问题可得解.
当最小元素为1,最大元素为72时,集合有如下情况:
集合只含2个元素:![]() 只有1种情况;
只有1种情况;
集合含有3个元素:![]() 且
且![]() ,共有
,共有![]() 种情况;
种情况;
集合含有4个元素:![]() 且
且![]() ,共有
,共有![]() 种情况;
种情况;
以此类推……
集合含有72个元素:![]() ,有(
,有(![]() )种情况.
)种情况.
所以,此类满足要求的子集元素个数之和M为:
![]()
![]()
![]()
①②两式对应项相加,得:
![]()
![]()
同理可得:![]() 所有子集元素个数之和都是
所有子集元素个数之和都是![]() ,所以集合
,所以集合![]() 所有直径为
所有直径为![]() 的子集的元素个数之和为
的子集的元素个数之和为![]() .
.
故选:C


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案科目:高中数学 来源: 题型:
【题目】某校![]() 名学生参加军事冬令营活动,活动期间各自扮演一名角色进行分组游戏,角色按级别从小到大共
名学生参加军事冬令营活动,活动期间各自扮演一名角色进行分组游戏,角色按级别从小到大共![]() 种,分别为士兵、排长、连长、营长、团长、旅长、师长、军长和司令.游戏分组有两种方式,可以
种,分别为士兵、排长、连长、营长、团长、旅长、师长、军长和司令.游戏分组有两种方式,可以![]() 人一组或者
人一组或者![]() 人一组.如果
人一组.如果![]() 人一组,则必须角色相同;如果
人一组,则必须角色相同;如果![]() 人一组,则
人一组,则![]() 人角色相同或者
人角色相同或者![]() 人为级别连续的
人为级别连续的![]() 个不同角色.已知这
个不同角色.已知这![]() 名学生扮演的角色有
名学生扮演的角色有![]() 名士兵和
名士兵和![]() 名司令,其余角色各
名司令,其余角色各![]() 人,现在新加入
人,现在新加入![]() 名学生,将这
名学生,将这![]() 名学生分成
名学生分成![]() 组进行游戏,则新加入的学生可以扮演的角色的种数为________.
组进行游戏,则新加入的学生可以扮演的角色的种数为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图![]() ,某十字路口的花圃中央有一个底面半径为
,某十字路口的花圃中央有一个底面半径为![]() 的圆柱形花柱,四周斑马线的内侧连线构成边长为
的圆柱形花柱,四周斑马线的内侧连线构成边长为![]() 的正方形.因工程需要,测量员将使用仪器沿斑马线的内侧进行测量,其中仪器
的正方形.因工程需要,测量员将使用仪器沿斑马线的内侧进行测量,其中仪器![]() 的移动速度为
的移动速度为![]() ,仪器
,仪器![]() 的移动速度为
的移动速度为![]() .若仪器
.若仪器![]() 与仪器
与仪器![]() 的对视光线被花柱阻挡,则称仪器
的对视光线被花柱阻挡,则称仪器![]() 在仪器
在仪器![]() 的“盲区”中.
的“盲区”中.



(1)如图![]() ,斑马线的内侧连线构成正方形
,斑马线的内侧连线构成正方形![]() ,仪器
,仪器![]() 在点
在点![]() 处,仪器
处,仪器![]() 在
在![]() 上距离点
上距离点![]()
![]() 处,试判断仪器
处,试判断仪器![]() 是否在仪器
是否在仪器![]() 的“盲区”中,并说明理由;
的“盲区”中,并说明理由;
(2)如图![]() ,斑马线的内侧连线构成正方形
,斑马线的内侧连线构成正方形![]() ,仪器
,仪器![]() 从点
从点![]() 出发向点
出发向点![]() 移动,同时仪器
移动,同时仪器![]() 从点
从点![]() 出发向点
出发向点![]() 移动,在这个移动过程中,仪器
移动,在这个移动过程中,仪器![]() 在仪器
在仪器![]() 的“盲区”中的时长为多少?
的“盲区”中的时长为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() :
: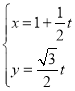 (
(![]() 为参数),曲线
为参数),曲线![]() :
:![]() (
(![]() 为参数).
为参数).
(1)设![]() 与
与![]() 相交于
相交于![]() 两点,求
两点,求![]() ;
;
(2)若把曲线![]() 上各点的横坐标压缩为原来的
上各点的横坐标压缩为原来的![]() 倍,纵坐标压缩为原来的
倍,纵坐标压缩为原来的![]() 倍,得到曲线
倍,得到曲线![]() ,设点P是曲线
,设点P是曲线![]() 上的一个动点,求它到直线
上的一个动点,求它到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线![]() ,直线l的参数方程为:
,直线l的参数方程为:![]() (t为参数),直线l与曲线C分别交于M,N两点.
(t为参数),直线l与曲线C分别交于M,N两点.
(1)写出曲线C和直线l的普通方程;
(2)若点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中有一分鹿问题:“今有大夫、不更、簪袅、上造、公士,凡五人,共猎得五鹿.欲以爵次分之,问各得几何.”在这个问题中,大夫、不更、簪袅、上造、公士是古代五个不同爵次的官员,现皇帝将大夫、不更、簪枭、上造、公士这5人分成两组(一组2人,一组3人),派去两地执行公务,则大夫、不更恰好在同一组的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方形![]() 、
、![]() 的边长都是1,而且平面
的边长都是1,而且平面![]() 、
、![]() 互相垂直.点M在
互相垂直.点M在![]() 上移动,点N在
上移动,点N在![]() 上移动,若
上移动,若![]() (
(![]() ).
).

(1)当a为何值时,![]() 的长最小;
的长最小;
(2)当![]() 长最小时,求面
长最小时,求面![]() 与面
与面![]() 所成的二面角α的余弦值.
所成的二面角α的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com