
【题目】已知 ![]() 的左、右焦点分别为
的左、右焦点分别为 ![]() ,
, ![]() ,点
,点 ![]() 在椭圆上,
在椭圆上, ![]() ,且
,且 ![]() 的面积为4.
的面积为4.
(1)求椭圆的方程;
(2)点 ![]() 是椭圆上任意一点,
是椭圆上任意一点, ![]() 分别是椭圆的左、右顶点,直线
分别是椭圆的左、右顶点,直线 ![]() 与直线
与直线 ![]() 分别交于
分别交于 ![]() 两点,试证:以
两点,试证:以 ![]() 为直径的圆交
为直径的圆交 ![]() 轴于定点,并求该定点的坐标.
轴于定点,并求该定点的坐标.
【答案】
(1)解;因为 ![]() ,所以
,所以 ![]() ,
, ![]() .
.
由题意得 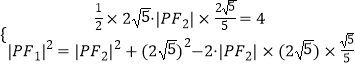 ,解得
,解得 ![]() .
.
从而 ![]() ,结合
,结合 ![]() ,得
,得 ![]() ,
,
故椭圆的方程为 ![]() .
.
(2)解:由(1)得 ![]() ,
, ![]() ,
,
设 ![]() ,则直线
,则直线 ![]() 的方程为
的方程为 ![]() ,
,
它与直线 ![]() 的交点的坐标为
的交点的坐标为 ![]() ,
,
直线 ![]() 的方程为
的方程为 ![]() ,它与直线
,它与直线 ![]() 的交点的坐标为
的交点的坐标为 ![]() ,
,
再设以 ![]() 为直径的圆交
为直径的圆交 ![]() 轴于点
轴于点 ![]() ,则
,则 ![]() ,从而
,从而 ![]() ,即
,即 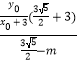
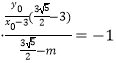 ,即
,即 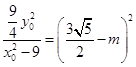 ,解得
,解得 ![]() .
.
故以 ![]() 为直径的圆交
为直径的圆交 ![]() 轴于定点,该定点的坐标为
轴于定点,该定点的坐标为 ![]() 或
或 ![]() .
.
【解析】(1) 由已知求出![]() PF2F1的正弦和余弦值,再利用面积公式
PF2F1的正弦和余弦值,再利用面积公式![]() 以及余弦定理
以及余弦定理![]() 可求得点P到两焦点的距离,求出a的值进而得到b的值故可求出椭圆的方程。(2)由(1)的方程求出两个定点的坐标,设出点M的坐标得到直线的方程,进而可求出点E、F的坐标,利用两条直线垂直斜率之积等于-1即可求出m的值。
可求得点P到两焦点的距离,求出a的值进而得到b的值故可求出椭圆的方程。(2)由(1)的方程求出两个定点的坐标,设出点M的坐标得到直线的方程,进而可求出点E、F的坐标,利用两条直线垂直斜率之积等于-1即可求出m的值。


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:高中数学 来源: 题型:
【题目】(本题满分12分)已知不等式ax2-3x+6>4的解集为{x|x<1或x>b},
(1)求a,b;
(2)解不等式ax2-(ac+b)x+bc<0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在考试测评中,常用难度曲线图来检测题目的质量,一般来说,全卷得分高的学生,在某道题目上的答对率也应较高,如果是某次数学测试压轴题的第1、2问得分难度曲线图,第1、2问满分均为6分,图中横坐标为分数段,纵坐标为该分数段的全体考生在第1、2问的平均难度,则下列说法正确的是( ) 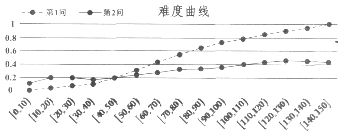
A.此题没有考生得12分
B.此题第1问比第2问更能区分学生数学成绩的好与坏
C.分数在[40,50)的考生此大题的平均得分大约为4.8分
D.全体考生第1问的得分标准差小于第2问的得分标准差
查看答案和解析>>
科目:高中数学 来源: 题型:
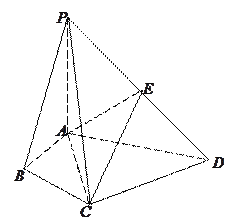
【题目】在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,![]() =2
=2![]() =2.
=2.
(1)求证:![]() ;
;
(2)求证:![]() ∥平面
∥平面![]() ;
;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知不等式|x+3|﹣2x﹣1<0的解集为(x0 , +∞)
(Ⅰ)求x0的值;
(Ⅱ)若函数f(x)=|x﹣m|+|x+ ![]() |﹣x0(m>0)有零点,求实数m的值.
|﹣x0(m>0)有零点,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】美索不达米亚平原是人类文明的发祥地之一.美索不达米亚人善于计算,他们创造了优良的计数系统,其中开平方算法是最具有代表性的.程序框图如图所示,若输入a,n,ξ的值分别为8,2,0.5,(每次运算都精确到小数点后两位)则输出结果为( ) 
A.2.81
B.2.82
C.2.83
D.2.84
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com