练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，在地上有同样大小的 5 块积木，一堆 2 个，一堆 3 个，要把积木一块一块的全部放到某个盒子里，每次 只能取出其中一堆最上面的一块，则不同的取法有______种（用数字作答）．

    【答案】10

    【解析】

    根据题意，假设左边的积木从上至下依次为1、2、3，右边的积木从上至下依次为4、5，分析可得必须先取1或4，据此分2种情况讨论，分别列举2种情况下的取法数目，由分类计数原理计算可得答案．

    解：根据题意，假设左边的积木从上至下依次为1、2、3，右边的积木从上至下依次为4、5，

    分2种情况讨论：

    若先取1，有12345、12453、12435、14235、14253、14523，共6种取法；

    若先取4，有45123、41523、41253、41235，共4种取法；

    则一共有中不同的取法；

    故答案为：10．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，四棱锥中，侧面为等边三角形且垂直于底面，，.

    （1）证明：平面；

    （2）若四棱锥的体积为，求的面积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知定义在上的奇函数满足，且时，，给出下列结论：①；②函数在上是增函数；③函数的图像关于直线对称；④若，则关于的方程在上的所有根之和为.则其中正确命题的序号为____________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

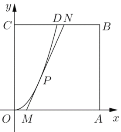
    【题目】某地要建造一个边长为2（单位：）的正方形市民休闲公园，将其中的区域开挖成一个池塘，如图建立平面直角坐标系后，点的坐标为，曲线是函数图像的一部分，过边上一点在区域内作一次函数（）的图像，与线段交于点（点不与点重合），且线段与曲线有且只有一个公共点，四边形为绿化风景区.

    （1）求证：；

    （2）设点的横坐标为，

    ①用表示、两点的坐标；

    ②将四边形的面积表示成关于的函数，并求的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知直线为椭圆的右准线，直线与轴的交点记为，过右焦点的直线与椭圆交于，两点.

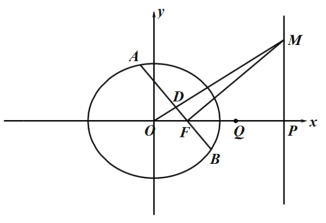
    （1）设点在直线上，且满足，若直线与线段交于点，求证：点为线段的中点；

    （2）设点的坐标为，直线与直线交于点，试问是否为定值，若是，求出这个定值，若不是，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数 F (x) = e x 满足 F ( x) = g ( x) + h( x) ，且 g ( x), h( x) 分别是定义在 R 上的偶函数和奇函数．

    （1）求函数 h(x)的反函数；

    （2）已知(x) = g(x 1)，若函数(x)在 [1,3]上满足(2 a+1) ，求实数 a 的取值范围；

    （3）若对于任意 x ∈(0,2]不等式 g(2x) ah(x) ≥ 0 恒成立，求实数 a 的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知甲、乙、丙三位同学在某次考试中总成绩列前三名，有，，三位学生对其排名猜测如下：：甲第一名，乙第二名；：丙第一名；甲第二名；：乙第一名，甲第三名.成绩公布后得知，，，三人都恰好猜对了一半，则第一名是__________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设，已知函数，.

    （Ⅰ）设，求在上的最大值.

    （Ⅱ）设，若的极大值恒小于0，求证：.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

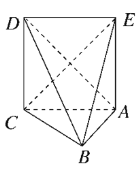
    【题目】如图，在三棱锥D－ABC中，底面ABC，为正三角形，若，，则三棱锥D－ABC与三棱锥E－ABC的公共部分构成的几何体的外接球的体积为（ ）

    A.B.C.D.

    查看答案和解析>>

    同步练习册答案