
【题目】2020年3月12日,国务院新闻办公室发布会重点介绍了改革开放40年,特别是党的十八大以来我国脱贫攻坚、精准扶贫取得的显著成绩,这些成绩为全面脱贫初步建成小康社会奠定了坚实的基础.下图是统计局公布的2010年~2019年年底的贫困人口和贫困发生率统计表.则下面结论正确的是( )
(年底贫困人口的线性回归方程为![]() (其中
(其中![]() 年份-2019),贫困发生率的线性回归方程为
年份-2019),贫困发生率的线性回归方程为![]() (其中
(其中![]() 年份-2009))
年份-2009))

A.2010年~2019年十年间脱贫人口逐年减少,贫困发生率逐年下降
B.2012年~2019年连续八年每年减贫超过1000万,且2019年贫困发生率最低
C.2010年~2019年十年间超过1.65亿人脱贫,其中2015年贫困发生率低于6%
D.根据图中趋势线可以预测,到2020年底我国将实现全面脱贫
【答案】BD
【解析】
根据统计表计算出每年脱贫的人口,由此判断出正确选项.
每年脱贫的人口如下表所示:
| 期初 | 期末 | 脱贫人口 |
2009年底至2010年年底 |
| 16566 |
|
2010年底至2011年年底 | 16566 | 12238 | 4328 |
2011年底至2012年年底 | 12238 | 9899 | 2339 |
2012年底至2013年年底 | 9899 | 8249 | 1650 |
2013年底至2014年年底 | 8249 | 7017 | 1232 |
2014年底至2015年年底 | 7017 | 5575 | 1442 |
2015年底至2016年年底 | 5575 | 4335 | 1240 |
2016年底至2017年年底 | 4335 | 3046 | 1289 |
2017年底至2018年年底 | 3046 | 1660 | 1386 |
2018年底至2019年年底 | 1660 | 551 | 1109 |
由于缺少![]() 年年底数据,故无法统计十年间脱贫人口的数据,故AC选项错误.
年年底数据,故无法统计十年间脱贫人口的数据,故AC选项错误.
根据上表可知:![]() 年~
年~![]() 年连续八年每年减贫超过
年连续八年每年减贫超过![]() 万,且
万,且![]() 年贫困发生率最低,故B选项正确.
年贫困发生率最低,故B选项正确.
根据上表可知,![]() 年~
年~![]() 年连续八年每年减贫超过
年连续八年每年减贫超过![]() 万,
万,![]() 年年底,贫困人口
年年底,贫困人口![]() 万,故预计到
万,故预计到![]() 年底我国将实现全面脱贫,故D选项正确.
年底我国将实现全面脱贫,故D选项正确.
综上所述,正确的选项为BD.
故选:BD


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:高中数学 来源: 题型:
【题目】随着我国经济结构调整和方式转变,社会对高质量人才的需求越来越大,因此考研现象在我国不断升温.某大学一学院甲、乙两个本科专业,研究生的报考和录取情况如下表,则
性别 | 甲专业报考人数 | 乙专业报考人数 | 性别 | 甲专业录取率 | 乙专业录取率 | |
男 | 100 | 400 | 男 |
|
| |
女 | 300 | 100 | 女 |
|
|
A.甲专业比乙专业的录取率高B.乙专业比甲专业的录取率高
C.男生比女生的录取率高D.女生比男生的录取率高
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c.已知a2+c2=b2![]() ac.
ac.
(1)求cosB及tan2B的值;
(2)若b=3,A![]() ,求c的值.
,求c的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 的左右焦点分别为
的左右焦点分别为![]() ,
,![]() 的周长为12.
的周长为12.
(1)求点![]() 的轨迹
的轨迹![]() 的方程.
的方程.
(2)已知点![]() ,是否存在过点
,是否存在过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于不同的两点
交于不同的两点![]() ,使得
,使得![]() ,若存在,求出直线
,若存在,求出直线![]() 的方程,若不存在,请说明理由.
的方程,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的圆柱![]() 中,AB为圆
中,AB为圆![]() 的直径,
的直径,![]() 是
是![]() 的两个三等分点,EA,FC,GB都是圆柱
的两个三等分点,EA,FC,GB都是圆柱![]() 的母线.
的母线.
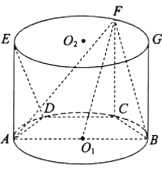
(1)求证:![]() 平面ADE;
平面ADE;
(2)设BC=1,已知直线AF与平面ACB所成的角为30°,求二面角A—FB—C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我们打印用的A4纸的长与宽的比约为![]() ,之所以是这个比值,是因为把纸张对折,得到的新纸的长与宽之比仍约为
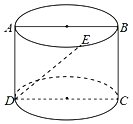
,之所以是这个比值,是因为把纸张对折,得到的新纸的长与宽之比仍约为![]() ,纸张的形状不变.已知圆柱的母线长小于底面圆的直径长(如图所示),它的轴截面ABCD为一张A4纸,若点E为上底面圆上弧AB的中点,则异面直线DE与AB所成的角约为( )
,纸张的形状不变.已知圆柱的母线长小于底面圆的直径长(如图所示),它的轴截面ABCD为一张A4纸,若点E为上底面圆上弧AB的中点,则异面直线DE与AB所成的角约为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,
,![]() ,其中
,其中![]() ,
,![]() 是自然对数的底数.
是自然对数的底数.
(1)若![]() 在
在![]() 上存在两个极值点,求
上存在两个极值点,求![]() 的取值范围;
的取值范围;
(2)若![]() ,
,![]() ,函数
,函数![]() 与函数
与函数![]() 的图象交于
的图象交于![]() ,
,![]() ,
,![]() ,
,![]() ,且
,且![]() 线段的中点为
线段的中点为![]() ,证明:
,证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在疫情这一特殊时期,教育行政部门部署了“停课不停学”的行动,全力帮助学生在线学习.复课后进行了摸底考试,某校数学教师为了调查高三学生这次摸底考试的数学成绩与在线学习数学时长之间的相关关系,对在校高三学生随机抽取45名进行调查.知道其中有25人每天在线学习数学的时长是不超过1小时的,得到了如下的等高条形图:
(1)是否有![]() 的把握认为“高三学生的这次摸底考试数学成绩与其在线学习时长有关”;
的把握认为“高三学生的这次摸底考试数学成绩与其在线学习时长有关”;
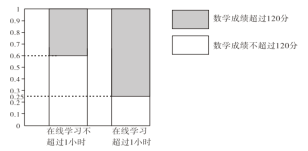
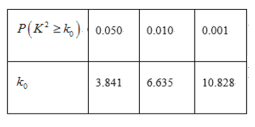
(2)将频率视为概率,从全校高三学生这次数学成绩超过120分的学生中随机抽取10人,求抽取的10人中每天在线学习时长超过1小时的人数的数学期望与方差.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com