
已知函数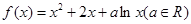 .当
.当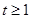 时,不等式
时,不等式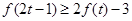 恒成立,则实数
恒成立,则实数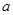 的取值范围是( )
的取值范围是( )
A.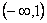 B.
B.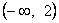 C.
C.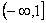 D.
D.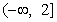
D
【解析】(Ⅱ)∵f(x)=x2+2x+alnx,
∴f(2t-1)≥2f(t)-3⇒2t2-4t+2≥2alnt-aln(2t-1)=aln[t2 /(2t-1 )).
当t≥1时,t2≥2t-1,∴ln[t2 /2t-1 ]≥0.即t>1时,a≤2(t-1)2 /(ln(t2 /2t-1)) 恒成立.又易证ln(1+x)≤x在x>-1上恒成立,
∴(ln(t2 /2t-1)) =ln[1+[(t-1)2/ 2t-1] ]≤(t-1)2 /(2t-1) <(t-1)2在t>1上恒成立.当t=1时取等号,∴当t≥1时,ln(t2 /2t-1) ≤(t-1)2,∴由上知a≤2.故实数a的取值范围是(-∞,2].


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源:2012-2013学年天津市高一(上)期末数学试卷(解析版) 题型:解答题
 )的图象如图所示.
)的图象如图所示. 个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的对称轴方程;
个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的对称轴方程;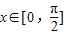 时,方程f(x)=2a-3有两个不等的实根x1,x2,求实数a的取值范围,并求此时x1+x2的值.
时,方程f(x)=2a-3有两个不等的实根x1,x2,求实数a的取值范围,并求此时x1+x2的值.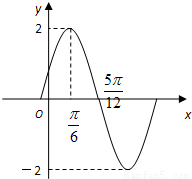
查看答案和解析>>
科目:高中数学 来源:2011-2012学年重庆市高三考前模拟测试理科数学试卷(解析版) 题型:解答题
已知函数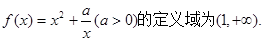
(I)讨论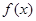 在其定义域上的单调性;
在其定义域上的单调性;
(II)当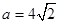 时,若关于x的方程
时,若关于x的方程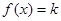 恰有两个不等实根,求实数k的取值范围。
恰有两个不等实根,求实数k的取值范围。
查看答案和解析>>
科目:高中数学 来源:2011-2012学年福建省高三高考模拟文科数学试卷(解析版) 题型:解答题
(本小题满分14分)
已知函数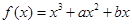
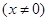 只有一个零点
只有一个零点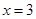 .
.
(Ⅰ)求函数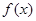 的解析式;
的解析式;
(Ⅱ)若函数 在区间
在区间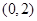 上有极值点,求
上有极值点,求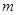 取值范围;
取值范围;
(Ⅲ)是否存在两个不等正数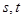
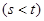 ,当
,当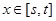 时,函数
时,函数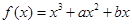 的值域也是
的值域也是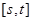 ,若存在,求出所有这样的正数
,若存在,求出所有这样的正数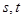 ;若不存在,请说明理由;
;若不存在,请说明理由;
查看答案和解析>>
科目:高中数学 来源: 题型:阅读理解
(本小题满分14分)
阅读下面一段文字:已知数列![]() 的首项
的首项![]() ,如果当
,如果当![]() 时,
时,![]() ,则易知通项
,则易知通项![]() ,前
,前![]() 项的和
项的和![]() . 将此命题中的“等号”改为“大于号”,我们得到:数列
. 将此命题中的“等号”改为“大于号”,我们得到:数列![]() 的首项
的首项![]() ,如果当
,如果当![]() 时,
时,![]() ,那么
,那么![]() ,且
,且![]() . 这种从“等”到“不等”的类比很有趣。由此还可以思考:要证
. 这种从“等”到“不等”的类比很有趣。由此还可以思考:要证![]() ,可以先证
,可以先证![]() ,而要证
,而要证![]() ,只需证
,只需证![]() (
(![]() ). 结合以上思想方法,完成下题:
). 结合以上思想方法,完成下题:
已知函数![]() ,数列
,数列![]() 满足
满足![]() ,
,![]() ,若数列
,若数列![]() 的前
的前![]() 项的和为
项的和为![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
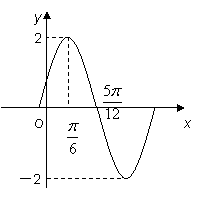
已知函数![]() (其中
(其中![]() )的图象如图所示.
)的图象如图所示.
(1)求![]() 的解析式;
的解析式;
(2)将函数![]() 的图象向右平移
的图象向右平移![]() 个单位后,再将得到的图象上各点的横坐标伸长到
个单位后,再将得到的图象上各点的横坐标伸长到
原来的![]() 倍,纵坐标不变,得到函数
倍,纵坐标不变,得到函数![]() 的图象,求
的图象,求![]() 的对称轴方程;
的对称轴方程;
 (3)当
(3)当![]() 时,方程
时,方程![]() 有两个不等的实根
有两个不等的实根![]() ,
,![]() ,求实数
,求实数![]() 的取值范围,
的取值范围,
并求此时![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com