
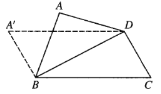
【题目】如图,矩形![]() 中,
中,![]() ,将
,将![]() 沿对角线
沿对角线![]() 向上翻折,若翻折过程中
向上翻折,若翻折过程中![]() 长度在
长度在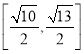 内变化,则点
内变化,则点![]() 所形成的运动轨迹的长度为__________.
所形成的运动轨迹的长度为__________.
 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:
【题目】动圆![]() 与圆
与圆![]() 外切,并与直线
外切,并与直线![]() 相切,则动圆圆心
相切,则动圆圆心![]() 的轨迹方程为__________,过点
的轨迹方程为__________,过点![]() 作倾斜角互补的两条直线,分别与圆心
作倾斜角互补的两条直线,分别与圆心![]() 的轨迹相交于
的轨迹相交于![]() ,
,![]() 两点,则直线
两点,则直线![]() 的斜率为__________.
的斜率为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为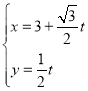 (
(![]() 为参数),在以坐标原点
为参数),在以坐标原点![]() 为极点、以
为极点、以![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,若直线
,若直线![]() 与曲线
与曲线![]() 交于
交于![]() 、
、![]() 两点.
两点.
(1)求线段![]() 的中点
的中点![]() 的直角坐标;
的直角坐标;
(2)设点![]() 是曲线
是曲线![]() 上任意一点,求
上任意一点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() .以
.以![]() ,
,![]() 为邻边作平行四边形
为邻边作平行四边形![]() ,连接
,连接![]() 和
和![]() .
.
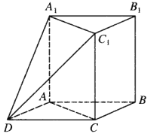
(1)求证:![]() 平面
平面![]() ;
;
(2)线段![]() 上是否存在点
上是否存在点![]() ,使平面
,使平面![]() 与平面
与平面![]() 垂直?若存在,求出
垂直?若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正方体![]() 的棱长为
的棱长为![]() ,
,![]() 为
为![]() 的中点,下列说法中正确的是( )
的中点,下列说法中正确的是( )
A.![]() 与
与![]() 所成的角大于
所成的角大于![]()
B.点![]() 到平面
到平面![]() 的距离为
的距离为![]()
C.三棱锥![]() 的外接球的表面积为
的外接球的表面积为![]()
D.直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,PA⊥平面ABCD,在四边形ABCD中,∠ABC=![]() ,AB=4,BC=3,CD=
,AB=4,BC=3,CD=![]() ,AD=2
,AD=2![]() ,PA=4.
,PA=4.
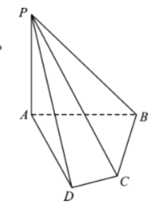
(1)证明:CD⊥平面PAD;
(2)求二面角B-PC-D的余弦值..
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校水果店有苹果、梨、香蕉、石榴、橘子、葡萄、西柚等![]() 种水果,西柚数量不多,只够一个人购买,甲乙丙丁戊
种水果,西柚数量不多,只够一个人购买,甲乙丙丁戊![]() 位同学去购买,每人只能选择其中一种,这
位同学去购买,每人只能选择其中一种,这![]() 位同学购买后,恰好买了其中三种水果,则他们购买水果的可能情况有___________种.
位同学购买后,恰好买了其中三种水果,则他们购买水果的可能情况有___________种.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,动圆
,动圆![]() 与圆
与圆![]() 外切,且与直线
外切,且与直线![]() 相切,该动圆圆心
相切,该动圆圆心![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程
的方程
(2)过点![]() 的直线与抛物线相交于
的直线与抛物线相交于![]() 两点,抛物线在点A的切线与
两点,抛物线在点A的切线与![]() 交于点N,求
交于点N,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com