
【题目】已知函数f (x)=lnx,g(x)=ex.
(1)若函数φ (x) = f (x)-![]() ,求函数φ (x)的单调增区间;
,求函数φ (x)的单调增区间;
(2)设直线l为函数的图象上一点A(x0,f (x0))处的切线.证明:在区间(1,+∞)上存在唯一的x0,使得直线l与曲线y=g(x)相切.
科目:高中数学 来源: 题型:
【题目】我校甲、乙、丙三名语文老师和![]() 、
、![]() 、
、![]() 三名数学老师被派往某县城一中和二中支教,其中有一名语文老师和一名数学老师被派到了一中,其它老师都去二中支教,则甲与
三名数学老师被派往某县城一中和二中支教,其中有一名语文老师和一名数学老师被派到了一中,其它老师都去二中支教,则甲与![]() 被派到同一所学校的概率为( )
被派到同一所学校的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图中(1)(2)(3)(4)为四个平面图形,表中给出了各平面图形中的顶点数边数以及区域数.
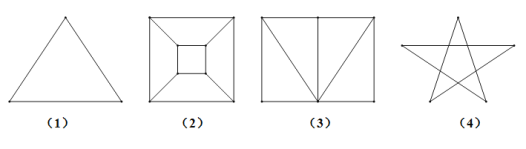
平面图形 | 顶点数 | 边数 | 区域数 |
1 | 3 | 3 | 2 |
2 | 8 | 12 | 6 |
3 | 6 | 9 | 5 |
4 | 10 | 15 | 7 |
现已知某个平面图形有1009个顶点,且围成了1006个区域,试根据以上关系确定这个平面图形的边数为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】农历五月初五是端午节,民间有吃粽子的习惯,粽子又称粽籺,古称“角黍”,平行四边形形状的纸片是由六个边长为![]() 的正三角形构成的,将它沿虚线折起来,可以得到如图所示粽子形状的六面体,则该六面体的体积为______;若该六面体内有一球,则该球表面积的最大值为______.
的正三角形构成的,将它沿虚线折起来,可以得到如图所示粽子形状的六面体,则该六面体的体积为______;若该六面体内有一球,则该球表面积的最大值为______.
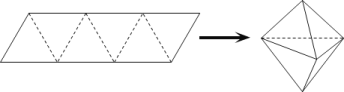
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】体温是人体健康状况的直接反应,一般认为成年人腋下温度T(单位:![]() )平均在
)平均在![]() 之间即为正常体温,超过
之间即为正常体温,超过![]() 即为发热.发热状态下,不同体温可分成以下三种发热类型:低热:
即为发热.发热状态下,不同体温可分成以下三种发热类型:低热:![]() ;高热:
;高热:![]() ;超高热(有生命危险):
;超高热(有生命危险):![]() .某位患者因患肺炎发热,于12日至26日住院治疗.医生根据病情变化,从14日开始,以3天为一个疗程,分别用三种不同的抗生素为该患者进行消炎退热.住院期间,患者每天上午8:00服药,护士每天下午16:00为患者测量腋下体温记录如下:
.某位患者因患肺炎发热,于12日至26日住院治疗.医生根据病情变化,从14日开始,以3天为一个疗程,分别用三种不同的抗生素为该患者进行消炎退热.住院期间,患者每天上午8:00服药,护士每天下午16:00为患者测量腋下体温记录如下:
抗生素使用情况 | 没有使用 | 使用“抗生素A”疗 | 使用“抗生素B”治疗 | |||||
日期 | 12日 | 13日 | 14日 | 15日 | 16日 | 17日 | 18日 | 19日 |
体温( | 38.7 | 39.4 | 39.7 | 40.1 | 39.9 | 39.2 | 38.9 | 39.0 |
抗生素使用情况 | 使用“抗生素C”治疗 | 没有使用 | |||||
日期 | 20日 | 21日 | 22日 | 23日 | 24日 | 25日 | 26日 |
体温( | 38.4 | 38.0 | 37.6 | 37.1 | 36.8 | 36.6 | 36.3 |
(I)请你计算住院期间该患者体温不低于![]() 的各天体温平均值;
的各天体温平均值;
(II)在19日—23日期间,医生会随机选取3天在测量体温的同时为该患者进行某一特殊项目“a项目”的检查,记X为高热体温下做“a项目”检查的天数,试求X的分布列与数学期望;
(III)抗生素治疗一般在服药后2-8个小时就能出现血液浓度的高峰,开始杀灭细菌,达到消炎退热效果.假设三种抗生素治疗效果相互独立,请依据表中数据,判断哪种抗生素治疗效果最佳,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com