
【题目】在直角梯形PBCD中, ![]() ,A为PD的中点,如下左图。将
,A为PD的中点,如下左图。将![]() 沿AB折到
沿AB折到![]() 的位置,使
的位置,使![]() ,点E在SD上,且
,点E在SD上,且![]() ,如下图。
,如下图。
(1)求证: ![]() 平面ABCD;
平面ABCD;
(2)求二面角E—AC—D的正切值.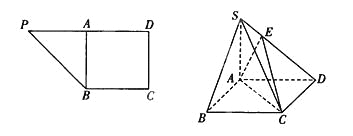
【答案】(1)在图中,由题意可知![]() 为正方形,所以在图中,
为正方形,所以在图中, ![]() ,
,
四边形ABCD是边长为2的正方形,
因为![]() ,AB
,AB![]() BC,
BC,
所以BC![]() 平面SAB,
平面SAB,
又![]() 平面SAB,所以BC
平面SAB,所以BC![]() SA,又SA
SA,又SA![]() AB,
AB,
所以SA![]() 平面ABCD,
平面ABCD,
(2)![]()
【解析】试题分析:(1)证明:在图中,由题意可知,

![]() 为正方形,所以在图中,
为正方形,所以在图中, ![]() ,
,
四边形ABCD是边长为2的正方形,
因为![]() ,AB
,AB![]() BC,
BC,
所以BC![]() 平面SAB,
平面SAB,
又![]() 平面SAB,所以BC
平面SAB,所以BC![]() SA,又SA
SA,又SA![]() AB,
AB,
所以SA![]() 平面ABCD,
平面ABCD,
(2)在AD上取一点O,使![]() ,连接EO。
,连接EO。
因为![]() ,所以EO//SA
,所以EO//SA
所以EO![]() 平面ABCD,过O作OH
平面ABCD,过O作OH![]() AC交AC于H,连接EH,
AC交AC于H,连接EH,
则AC![]() 平面EOH,所以AC
平面EOH,所以AC![]() EH。
EH。
所以![]() 为二面角E—AC—D的平面角,
为二面角E—AC—D的平面角,
![]() 在
在![]() 中,
中, ![]() …11分
…11分
![]() ,即二面角E—AC—D的正切值为
,即二面角E—AC—D的正切值为![]()


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在极坐标系中,曲线![]() :
:![]() ,以极点
,以极点![]() 为原点,极轴为
为原点,极轴为![]() 轴的正半轴建立平面直角坐标系,过点
轴的正半轴建立平面直角坐标系,过点![]() 的直线
的直线![]() 的参数方程为
的参数方程为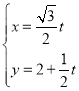 (
(![]() 为参数),点
为参数),点![]() 在直线
在直线![]() 上,且
上,且![]() .
.
(Ⅰ)求点![]() 的极坐标;
的极坐标;
(Ⅱ)若点![]() 是曲线
是曲线![]() 上一动点,求点
上一动点,求点![]() 到直线
到直线![]() 的距离的最小值.
的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分14分)如图,在三棱锥P- ABC中,已知平面PBC![]() 平面ABC.
平面ABC.
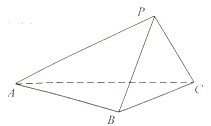
(1)若AB![]() BC,CP
BC,CP![]() PB,求证:CP
PB,求证:CP![]() PA:
PA:
(2)若过点A作直线![]() ⊥平面ABC,求证:
⊥平面ABC,求证: ![]() //平面PBC.
//平面PBC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念,记交通指数为T.其范围为[0,10],分别有五个级别:T∈[0,2)畅通;T∈[2,4)基本畅通;T∈[4,6)轻度拥堵;T∈[6,8)中度拥堵;T∈[8,10]严重拥堵,晚高峰时段(T≥2),从某市交通指挥中心选取了市区20个交通路段,依据其交通指数数据绘制的部分直方图如图所示.
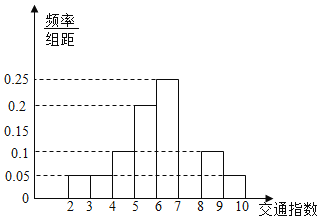
(1)请补全直方图,并求出轻度拥堵、中度拥堵、严重拥堵路段各有多少个?
(2)用分层抽样的方法从交通指数在[4,6),[6,8),[8,l0]的路段中共抽取6个路段,求依次抽取的三个级别路段的个数;
(3)从(2)中抽出的6个路段中任取2个,求至少一个路段为轻度拥堵的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角梯形PBCD中,∠D=∠C![]() ,BC=CD=2,PD=4,A为PD的中点,如图1,将△PAB沿AB折到△SAB的位置,使SB⊥BC,点E在SD上,如图2.
,BC=CD=2,PD=4,A为PD的中点,如图1,将△PAB沿AB折到△SAB的位置,使SB⊥BC,点E在SD上,如图2.
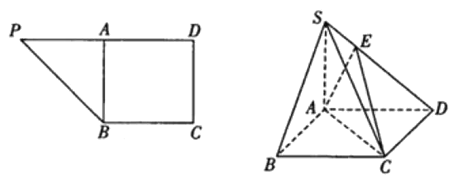
(1)求证:SA⊥平面ABCD;
(2)若E为SD中点,求D点到面EAC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如右图,一个直径为1的小圆沿着直径为2的大圆内壁的逆时针方
向滚动,M和N是小圆的一条固定直径的两个端点.那么,当小圆这
样滚过大圆内壁的一周,点M,N在大圆内所绘出的图形大致是( )
A.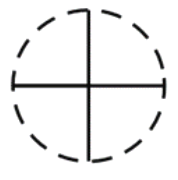 B.
B.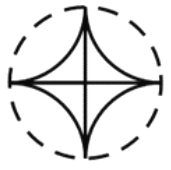
C. D.
D.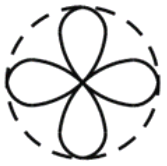
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的离心率
的离心率![]() ,且点
,且点![]() 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)若点![]() 都在椭圆
都在椭圆![]() 上,且
上,且![]() 中点
中点![]() 在线段
在线段![]() (不包括端点)上.
(不包括端点)上.
①求直线![]() 的斜率;
的斜率;
②求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com