
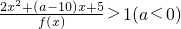 .
. 且开口向上.
且开口向上. .
. .(6分)
.(6分) ,∴x<0或
,∴x<0或 .(8分)
.(8分) ,
, .(11分)
.(11分) ;
; .(12分)
.(12分) ;进而得到x(x-5)(ax+5)>0;再通过讨论几个根的大小即可得到不等式的解集.
;进而得到x(x-5)(ax+5)>0;再通过讨论几个根的大小即可得到不等式的解集.

科目:高中数学 来源: 题型:
| ||
| 2 |
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2009年浙江省温州市摇篮杯高一数学竞赛试卷(解析版) 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2009-2010学年重庆外国语学校高一(上)期末数学试卷(解析版) 题型:选择题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com