
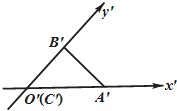
 水平放置的△ABC由“斜二测画法”画得的直观图如图所示,已知A′C′=3,B′C′=2,则AB边的实际长度为( )
水平放置的△ABC由“斜二测画法”画得的直观图如图所示,已知A′C′=3,B′C′=2,则AB边的实际长度为( )A、
| ||
| B、5 | ||
C、
| ||
| D、2 |
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案科目:高中数学 来源: 题型:
| a+b |
| 2 |
| ab |
| ab |
| A、P=M∩N |
| B、P=M∩(∁UN) |
| C、P=(∁UM)∩N |
| D、P=M∪N |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 年级 | 相关人数 | 抽取人数 |
| 高一 | 18 | x |
| 高二 | 36 | 2 |
| 高三 | 54 | y |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com