
����Ŀ��ij����ÿ����ÿ֦5Ԫ�ļ۸��ũ����������֦õ�廨��Ȼ����ÿ֦10Ԫ�ļ۸���ۣ�������������꣬ʣ�µ�õ�廨������������
��1��������һ�칺��16֦õ�廨�����������y����λ��Ԫ�����ڵ���������n����λ��֦��n��N���ĺ�������ʽ��
��2�������¼��100��õ�廨��������������λ��֦�����������±���
��������n | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
Ƶ�� | 10 | 20 | 16 | 16 | 15 | 13 | 10 |
��100���¼�ĸ���������Ƶ����Ϊ�������������ĸ��ʣ�
��i��������һ�칺��16֦õ�廨��X��ʾ���������λ��Ԫ������X�ķֲ��У���ѧ���������
��ii��������ƻ�һ�칺��16֦��17֦õ�廨������ΪӦ����16֦����17֦����˵�����ɣ�
���𰸡�
��1���⣺��n��16ʱ��y=16����10��5��=80��
��n��15ʱ��y=5n��5��16��n��=10n��80���ã� ![]()
��2���⣺��i��X��ȡ60��70��80������������n=14ʱ��X=60��n=15ʱ��X=70���������X=80��
P��X=60��= ![]() =
= ![]() =0.1��P��X=70��=
=0.1��P��X=70��= ![]() 0.2��P��X=80��=1��0.1��0.2=0.7��
0.2��P��X=80��=1��0.1��0.2=0.7��
X�ķֲ���Ϊ
X | 60 | 70 | 80 |
P | 0.1 | 0.2 | 0.7 |
EX=60��0.1+70��0.2+80��0.7=76
DX=162��0.1+62��0.2+42��0.7=44
��ii������17֦ʱ����������������Ϊy=��14��5��3��5����0.1+��15��5��2��5����0.2+��16��5��1��5����0.16+17��5��0.54=76.4
��76.4��76����Ӧ����17֦
����������1����������һ֦�ɵ�����5Ԫ��������һ֦�ɵ��Ȿ5Ԫ�����ɽ����ֶκ�������2����i��X��ȡ60��70��80��������Ӧ�ĸ��ʣ����ɵõ�X�ķֲ��У���ѧ�����������ii�������17֦ʱ����������빺��16֦õ�廨ʱ���������Ƚϣ����ɵõ����ۣ�


 ѧ���������ν��Ͼ���ѧ������ϵ�д�
ѧ���������ν��Ͼ���ѧ������ϵ�д� Happy holiday���ּ��������ҵ�㶫���������ϵ�д�
Happy holiday���ּ��������ҵ�㶫���������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڶ�����ABCDEF�У��ı���ABCD�������Σ�EF��AB��EF��FB��AB=2EF����BFC=90�㣬BF=FC��HΪBC���е㣮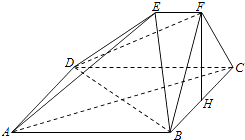
��1����֤��FH��ƽ��EDB��
��2����֤��AC��ƽ��EDB��
��3���⣺������B��DE��C�Ĵ�С��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ż����f��x���Ķ�����ΪR�����ڣ����ޣ�0����������������f���� ![]() ����f��a2��a+1���Ĵ�С��ϵΪ�� ��
����f��a2��a+1���Ĵ�С��ϵΪ�� ��
A.f���� ![]() ����f��a2��a+1��
����f��a2��a+1��
B.f���� ![]() ����f��a2��a+1��??
����f��a2��a+1��??
C.f���� ![]() ����f��a2��a+1��
����f��a2��a+1��
D.f���� ![]() ����f��a2��a+1��
����f��a2��a+1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ������
������![]() ��
��
��������![]() ʱ��������
ʱ��������![]() �ڵ�
�ڵ�![]() �������߷�����
�������߷�����
������![]() ������
������![]() �ϵ���Сֵ��������
�ϵ���Сֵ��������![]() ����Ȼ�����ĵ�����
����Ȼ�����ĵ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪f��x���Ƕ�����R�ϵ�ż��������x��0ʱ��f��x��=ax��a��1����
��1������f��x���Ľ���ʽ��
��2��������ʽf��x����4�Ľ⼯Ϊ[��2��2]����a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() �У���֪Բ
�У���֪Բ![]() ����Բ
����Բ![]() ��
�� ![]() Ϊ��Բ
Ϊ��Բ![]() ���Ҷ��㣬��ԭ��������
���Ҷ��㣬��ԭ��������![]() ���ֱ������Բ
���ֱ������Բ![]() ����
����![]() ���㣬
���㣬 ![]() ��
��![]() ����Ϸ���ֱ��
����Ϸ���ֱ��![]() ��Բ
��Բ![]() ����һ����Ϊ
����һ����Ϊ![]() ��ֱ��
��ֱ��![]() ��Բ
��Բ![]() ����һ����Ϊ
����һ����Ϊ![]() ��
��
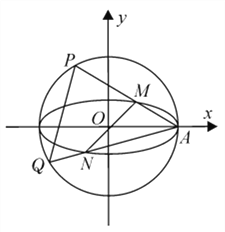
��1����![]() ����ֱ��
����ֱ��![]() ��б�ʣ�
��б�ʣ�
��2����![]() ��
��![]() ������ֱ�Ϊ
������ֱ�Ϊ![]() ����
����![]() �����ֵ.
�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������{an}���㣺a1= ![]() ��ǰn���Sn=
��ǰn���Sn= ![]() an ��
an ��
��1���a2 �� a3 �� a4��
��2���³�an�ı���ʽ��������ѧ���ɷ�֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����ֱ������ABCD�У�AB��CD����BCD=90�㣬BC=CD=2��AF=BF��EC��FD��FD�͵���ABCD��M��AB���е㣮 
��1����֤��ƽ��CFM��ƽ��BDF��
��2����N��CE�ϣ�EC=2��FD=3����CNΪ��ֵʱ��MN��ƽ��BEF��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ�뾶Ϊ2�İ�Բ��ֽ��ü��ɵ�������ABCD����״���µ�AB�ǰ�Բ��ֱ�����ϵ�CD�Ķ˵���Բ���ϣ�������������������ֵΪ��������
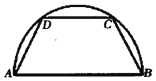
A. 3![]() B. 3
B. 3![]() C. 5
C. 5![]() D. 5
D. 5![]()
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com