练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】己知函数是定义在R上的周期为2的奇函数，时，，的值是____.

    【答案】

    【解析】

    根据题意，由函数的奇偶性与周期性分析可得f（﹣）＝f（﹣）＝﹣f（），结合解析式求出f（）的值，又因为f（2019）＝f（1+2×1009）＝f（1）＝0；据此分析可得答案．

    解：根据题意，函数f（x）是定义在R上的周期为2的奇函数，

    则f（﹣）＝f（﹣）＝﹣f（），

    f（2019）＝f（1+2×1009）＝f（1），

    又由函数f（x）是定义在R上的周期为2的奇函数，则有f（1）＝f（﹣1）且f（1）＝﹣f（﹣1），故f（1）＝0，则f（2019）＝0

    ，又由0＜x＜l时，f（x）＝4x，则f（）＝＝2，则f（﹣）＝﹣f（）＝﹣2；

    则＝﹣2；

    故答案为：﹣2

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】设△ABC面积的大小为S，且3 =2S．
    （1）求sinA的值；
    （2）若C= ， =16，求AC．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在△ABC中，DC⊥AB于D，BE⊥AC于E，BE交DC于点F，若BF=FC=3，DF=FE=2．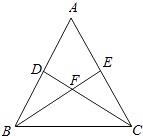

    （1）求证：ADAB=AEAC；
    （2）求线段BC的长度．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知四边形ABCD和BCEG均为直角梯形，AD∥BC，CE∥BG，且 ，平面ABCD⊥平面BCEG，BC=CD=CE=2AD=2BG=2

    （1）证明：AG∥平面BDE；
    （2）求平面BDE和平面BAG所成锐二面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】二项式的展开式中只有第6项的二项式系数最大，且展开式中的第3项的系数是第4项的系数的3倍，则的值为（ ）

    A. 4 B. 8 C. 12 D. 16

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】用长度分别为的四根木条围成一个平面四边形，则该平面四边形面积的最大值是____.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某企业生产一种产品，根据经验，其次品率与日产量 （万件）之间满足关系, （其中为常数，且，已知每生产1万件合格的产品以盈利2万元，但每生产1万件次品将亏损1万元（注:次品率=次品数/生产量， 如表示每生产10件产品，有1件次品，其余为合格品）.

    （1）试将生产这种产品每天的盈利额 （万元）表示为日产量 （万件）的函数；

    （2）当日产量为多少时，可获得最大利润?

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数f（x）=sinωx（ω＞0），将f（x）的图象向左平移 个单位从长度后，所得图象与原函数的图象重合，则ω的最小值为（ ）
    A.
    B.3
    C.6
    D.9

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】用数学归纳法证明，则当时，等式左边应在的基础上加上（ ）

    A. B.

    C. D.

    查看答案和解析>>

    同步练习册答案