
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)若函数![]() 有零点,求
有零点,求![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】如图,在下列四个正方体中,A,B为正方体的两个顶点,M,N,Q为所在棱的中点,则在这四个正方体中,直线AB与平面MNQ不垂直的是![]()
![]()
A. 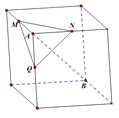 B.
B. 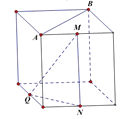
C. 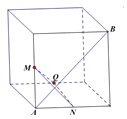 D.
D. 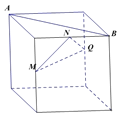
查看答案和解析>>
科目:高中数学 来源: 题型:
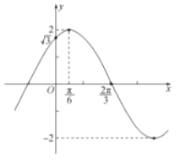
【题目】已知函数![]() 的图象如图所示,令
的图象如图所示,令![]() ,则下列关于函数
,则下列关于函数![]() 的说法中不正确的是( )
的说法中不正确的是( )
A. 函数![]() 图象的对称轴方程为
图象的对称轴方程为![]()
B. 函数![]() 的最大值为
的最大值为![]()
C. 函数![]() 的图象上存在点
的图象上存在点![]() ,使得在
,使得在![]() 点处的切线与直线
点处的切线与直线![]() :
:![]() 平行
平行
D. 方程![]() 的两个不同的解分别为
的两个不同的解分别为![]() ,
,![]() ,则
,则![]() 最小值为
最小值为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 中,底面
中,底面![]() 为平行四边形,
为平行四边形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 点在底面
点在底面![]() 内的射影
内的射影![]() 在线段
在线段![]() 上,且
上,且![]() ,
, ![]() ,M在线段
,M在线段![]() 上,且
上,且![]() .
.
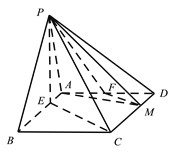
(Ⅰ)证明: ![]() 平面
平面![]() ;
;
(Ⅱ)在线段AD上确定一点F,使得平面![]() 平面PAB,并求三棱锥
平面PAB,并求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某乐园按时段收费,收费标准为:每玩一次不超过![]() 小时收费10元,超过
小时收费10元,超过![]() 小时的部分每小时收费
小时的部分每小时收费![]() 元(不足
元(不足![]() 小时的部分按
小时的部分按![]() 小时计算).现有甲、乙二人参与但都不超过
小时计算).现有甲、乙二人参与但都不超过![]() 小时,甲、乙二人在每个时段离场是等可能的。为吸引顾客,每个顾客可以参加一次抽奖活动。
小时,甲、乙二人在每个时段离场是等可能的。为吸引顾客,每个顾客可以参加一次抽奖活动。
(1) 用![]() 表示甲乙玩都不超过
表示甲乙玩都不超过![]() 小时的付费情况,求甲、乙二人付费之和为44元的概率;
小时的付费情况,求甲、乙二人付费之和为44元的概率;
(2)抽奖活动的规则是:顾客通过操作按键使电脑自动产生两个[0,1]之间的均匀随机数![]() ,并按如右所示的程序框图执行.若电脑显示“中奖”,则该顾客中奖;若电脑显示“谢谢”,则不中奖,求顾客中奖的概率.
,并按如右所示的程序框图执行.若电脑显示“中奖”,则该顾客中奖;若电脑显示“谢谢”,则不中奖,求顾客中奖的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据指令![]() (
(![]() ,
,![]() ),机器人在平面上能完成下列动作,先原地旋转弧度
),机器人在平面上能完成下列动作,先原地旋转弧度![]() (
(![]() 为正时,按逆时针方向旋转
为正时,按逆时针方向旋转![]() ,
,![]() 为负时,按顺时针方向旋转
为负时,按顺时针方向旋转![]() ),再朝其面对的方向沿直线行走距离r;
),再朝其面对的方向沿直线行走距离r;
(1)现机器人在平面直角坐标系的坐标原点,且面对x轴正方向,试给机器人下一个指令,使其移动到点![]() ;
;
(2)机器人在完成该指令后,发现在点![]() 处有一小球,正向坐标原点作匀速直线滚动,已知小球滚动的速度为机器人直线行走速度的2倍,若忽略机器人原地旋转所需的时间,问机器人最快可在何处截住小球?并给出机器人截住小球所需的指令?(结果用反三角函数表示)
处有一小球,正向坐标原点作匀速直线滚动,已知小球滚动的速度为机器人直线行走速度的2倍,若忽略机器人原地旋转所需的时间,问机器人最快可在何处截住小球?并给出机器人截住小球所需的指令?(结果用反三角函数表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com