已知集合A={x|-2<x<3},B={x|m<x<m+8}
(1)若A∪B=B,求m的取值范围,
(2)若A∩B≠∅,求出m的取值范围.
解:(1)集合A={x|-2<x<3},B={x|m<x<m+8}
由A∪B=B?A⊆B,
要使A⊆B,则需

,解得:-5≤m≤-2.
所以使A∪B=B的实数m的取值范围是[-5,-2];
(2)由A∩B≠∅,所以
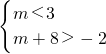
,解得:-10<m<3,
所以使A∩B=∅的实数m的取值范围是(-10,3).
分析:(1)首先根据A∪B=B得到A是B的子集,然后得出关于m的不等关系求解即可;
(2)由A∩B≠∅,得到A与B有公共元素,根据两集合端点值的关系列式求解m的范围.
点评:本题考查了子集与交集、并集运算的转换,考查了等价转化的数学思想,解答此题的关键是把并集与交集的关系转化为子集的关系,属基础题.
