
【题目】(题文)已知椭圆![]() 的离心率为
的离心率为![]() ,过点
,过点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 与
与![]() 两点,
两点,![]() ,且当直线
,且当直线![]() 垂直于
垂直于![]() 轴时,
轴时,![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若![]() ,求弦长
,求弦长![]() 的取值范围.
的取值范围.
【答案】(1) ![]() .
.
(2) ![]() .
.
【解析】
试题分析:圆锥曲线中求范围问题的关键是建立求解关于某个变量的目标函数,通过求这个函数的值域确定目标的范围.在建立函数的过程中要根据题目的其他已知条件,把需要的量都用我们选用的变量表示,有时为了运算的方便,在建立关系的过程中也可以采用多个变量,只要在最后结果中把多变量归结为单变量即可,同时要特别注意变量的取值范围.
试题解析:(Ⅰ)由已知:![]() ,
,![]() ,
,
又当直线垂直于![]() 轴时,
轴时,![]() ,所以椭圆过点
,所以椭圆过点![]() ,
,
代入椭圆:![]() ,
,
在椭圆中知:![]() ,联立方程组可得:
,联立方程组可得:![]() ,
,
所以椭圆![]() 的方程为:
的方程为:![]() .
.
(Ⅱ)当过点![]() 直线斜率为0时,点
直线斜率为0时,点![]() 、
、![]() 分别为椭圆长轴的端点,
分别为椭圆长轴的端点,
![]() 或
或![]() ,不合题意.
,不合题意.
所以直线的斜率不能为0.
可设直线方程为:![]()
![]() ,
,
将直线方程代入椭圆得:
![]() ,由韦达定理可得:
,由韦达定理可得:
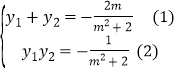 ,
,
将(1)式平方除以(2)式可得:
由已知![]() 可知,
可知,![]() ,
,
![]() ,
,
所以![]() ,
,
又知![]() ,
,![]() ,
,
![]() ,解得:
,解得:![]() .
.
![]()
![]()
![]()
![]() ,
,![]() ,
,
![]() .
.


 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:
【题目】针对某地区的一种传染病与饮用水进行抽样调查发现:饮用干净水得病5人,不得病50人;饮用不干净水得病9人,不得病22人。
(1)作出2×2列联表
(2)能否有90%的把握认为该地区中得传染病与饮用水有关?
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司研发芯片耗费资金2千万元,现在准备投入资金进行生产.经市场调查与预测,生产A芯片的毛收入![]() (平万元)与投入的资金x(千万元)成正比,已知每投入1千万元,获得毛收入0.25千万元;生产B芯片的毛收入
(平万元)与投入的资金x(千万元)成正比,已知每投入1千万元,获得毛收入0.25千万元;生产B芯片的毛收入![]() (千万元)与投入的资金x(千万元)的函数关系式为
(千万元)与投入的资金x(千万元)的函数关系式为![]() ,其图像如图所示.
,其图像如图所示.

(1)试分别求出生产A,B两种芯片的毛收入与投入资金的函数关系式.
(2)如果公司只生产一种芯片,生产哪种芯片毛收入更大?
(3)现在公司准备投入4亿元资金同时生产A,B两种芯片,设投入x千万元生产B芯片,用![]() 表示公司所获利润,当x为多少时,可以获得最大利润?并求最大利润.(利润=A芯片毛收入+B芯片毛收入-研发耗费资金)
表示公司所获利润,当x为多少时,可以获得最大利润?并求最大利润.(利润=A芯片毛收入+B芯片毛收入-研发耗费资金)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 是矩形,面
是矩形,面![]() 面
面![]() ,且
,且![]() 是边长为2的等边三角形,
是边长为2的等边三角形, ![]() ,
, ![]() 在
在![]() 上,且
上,且![]() 面
面![]()
(1)求证: ![]() 是
是![]() 的中点;
的中点;
(2)求直线![]() 与
与![]() 所成角的正切值;
所成角的正切值;
(3)在![]() 上是否存在点
上是否存在点![]() ,使二面角
,使二面角![]() 为直角?若存在,求出
为直角?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
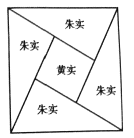
【题目】在古代,直角三角形中较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.三国时期吴国数学家赵爽用“弦图”( 如图) 证明了勾股定理,证明方法叙述为:“按弦图,又可以勾股相乘为朱实二,倍之为朱实四,以勾股之差自相乘为中黄实,加差实,亦成弦实.”这里的“实”可以理解为面积.这个证明过程体现的是这样一个等量关系:“两条直角边的乘积是两个全等直角三角形的面积的和(朱实二 ),4个全等的直角三角形的面积的和(朱实四) 加上中间小正方形的面积(黄实) 等于大正方形的面积(弦实)”. 若弦图中“弦实”为16,“朱实一”为![]() ,现随机向弦图内投入一粒黄豆(大小忽略不计),则其落入小正方形内的概率为( )
,现随机向弦图内投入一粒黄豆(大小忽略不计),则其落入小正方形内的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂现有职工320人,平均每人每年可创利20万元.该工厂打算购进一批智能机器人(每购进一台机器人,将有一名职工下岗).据测算,如果购进智能机器人不超过100台,每购进一台机器人,所有留岗职工(机器人视为机器,不作为职工看待)在机器人的帮助下,每人每年多创利2千元,每台机器人购置费及日常维护费用折合后平均每年2万元,工厂为体现对职工的关心,给予下岗职工每人每年4万元补贴;如果购进智能机器人数量超过100台,则工厂的年利润![]() 万元(x为机器人台数且x<320).
万元(x为机器人台数且x<320).
(1)写出工厂的年利润y与购进智能机器人台数x的函数关系.
(2)为获得最大经济效益,工厂应购进多少台智能机器人?此时工厂的最大年利润是多少?(参考数据:![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】元旦晚会期间,高三二班的学生准备了6 个参赛节目,其中有 2 个舞蹈节目,2 个小品节目,2个歌曲节目,要求歌曲节目一定排在首尾,另外2个舞蹈节目一定要排在一起,则这 6 个节目的不同编排种数为
A. 48 B. 36 C. 24 D. 12
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的焦距为
的焦距为![]() ,且
,且![]() 过点
过点![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设![]() 分别是椭圆
分别是椭圆![]() 的下顶点和上顶点,
的下顶点和上顶点, ![]() 是椭圆上异于
是椭圆上异于![]() 的任意一点,过点
的任意一点,过点![]() 作
作![]() 轴于
轴于![]() 为线段
为线段![]() 的中点,直线
的中点,直线![]() 与直线
与直线![]() 交于点
交于点![]() 为线段
为线段![]() 的中点,
的中点, ![]() 为坐标原点,求证:
为坐标原点,求证: ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com