
【题目】如图,一个侧棱长为![]() 的直三棱柱
的直三棱柱![]() 容器中盛有液体(不计容器厚度).若液面恰好分别过棱
容器中盛有液体(不计容器厚度).若液面恰好分别过棱![]() 中点
中点![]() .
.
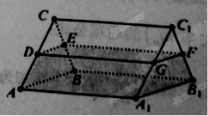
(1)求证:平面![]() 平面
平面![]() ;
;
(2)当底面![]() 水平放置时,求液面的高.
水平放置时,求液面的高.
【答案】(1)证明见解析;(2)液面的高为![]() .
.
【解析】
试题分析:(1)利用面面平行的判定定理:如果一个平面内有两条相交直线与另外一个平面平行,则这两个平面平行. 通过证明![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,得出平面
,得出平面![]() 平面
平面![]() ;(2)利用两种状态下体积相等,求出液面的高.
;(2)利用两种状态下体积相等,求出液面的高.
试题解析: (1)证明:∵![]() 分别为
分别为![]() 的中点,∴
的中点,∴![]() 是
是![]() 的中位线,∴
的中位线,∴![]() .
.
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ,
,
同理![]() 平面
平面![]() ,又
,又![]() ,∴平面
,∴平面![]() 平面
平面![]() .
.
(2)解:当直三棱柱![]() 容器侧面
容器侧面![]() 水平放置时,由(1)可知,液体部分是直四棱柱,其高即为原直三棱柱
水平放置时,由(1)可知,液体部分是直四棱柱,其高即为原直三棱柱![]() 容器的高,即侧棱长
容器的高,即侧棱长![]() .
.
当底面![]() 水平放置时,设液面的高为
水平放置时,设液面的高为![]() ,
,![]() 的面积为
的面积为![]() ,
,
由已知条件可知,![]() ∽
∽![]() ,且
,且![]() ,∴
,∴![]() .
.
由于两种状态下液体体积相等,∴![]() ,即
,即![]() .
.
因此,当底面![]() 水平放置时,液面的高为
水平放置时,液面的高为![]() .
.


科目:高中数学 来源: 题型:
【题目】读下面的甲、乙两个程序:
i=1;
S=0;
while i<=1000
S=S+i;
i=i+1;
end
甲
i=1000;
S=0;
for i=1000:-1:1
S=S+i;
end
乙
对甲、乙两个程序和输出的结果判断正确的是( )
A. 程序不同,结果不同
B. 程序不同,结果相同
C. 程序相同,结果不同
D. 程序相同,结果相同
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对一个容量为N的总体抽取容量为n的样本,当选取简单随机抽样、系统抽样和分层抽样三种不同方法抽取样本时,总体中每个个体被抽中的概率分别为P1,P2,P3,则
A. P1=P2<P3 B. P2=P3<P1 C. P1=P3<P2 D. P1=P2=P3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,满足: ①截 y 轴所得弦长为
,满足: ①截 y 轴所得弦长为![]() ; ②被
; ②被![]() 轴分成两段圆弧,其弧长的比为
轴分成两段圆弧,其弧长的比为![]() .
.
(1)求在满足条件①②的所有圆中,使代数式 ![]() 取得最小值时,圆的方程;
取得最小值时,圆的方程;
(2)在(1)中, ![]() 是圆上的任意一点,求
是圆上的任意一点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着手机的发展,“微信”越来越成为人们交流的一种方式.某机构对“使用微信交流”的态度进行调查,随机抽取了50人,他们年龄的频数分布及对“使用微信交流”赞成人数如下表.
年龄(单位:岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 5 | 10 | 12 | 7 | 2 | 1 |
(1)若以“年龄45岁为分界点”,由以上统计数据完成下面![]() 列联表,并判断是否有99%的把握认为“使用微信交流”的态度与人的年龄有关;
列联表,并判断是否有99%的把握认为“使用微信交流”的态度与人的年龄有关;
年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
赞成 | |||
不赞成 | |||
合计 |
(2)若从年龄在[55,65)的被调查人中随机选取2人进行追踪调查,求2人中至少有1人不赞成“使用微信交流”的概率.
参考数据如下:

![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com