练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    对定义在［-1,1］上的函数f(x),若存在常数A＞0,使得对任意x1、x2∈［-1,1］,都有|f(x1)-f(x2)|≤A·|x1-x2|,则称f(x)具有性质L.问函数f(x)=x2+3x+5与g(x)=|是否具有性质L?试证明之.

    思路分析:要确定一个函数具有性质L,其关键是要能找到满足题设条件中的常数A,而要确定一个函数不具有性质L,则一般需通过反证法来证明或寻找一个反例.

    解析:(1)对于f(x)=x2+3x+5,任取x1、x2∈［-1,1］,

    |f(x1)-f(x2)|=|x12-x22+3(x1-x2)|=|(x1-x2)(x1+x2+3)|

    =|x1-x2|·|x1+x2+3|

    ≤|x1-x2|·(|x1|+|x2|+3)

    ≤5|x1-x2|.

    ∴存在A=5,使f(x)具有性质L.

    (2)对于g(x)=,设它具有性质L,任取x1、x2∈［0,1］,则|g(x1)-g(x2)|=|-|

    =≤A|x1-x2|,

    ∴A≥,

    ≤2.

    ∴∈(0,2］.取x1=≤1,x2=,有,与≥矛盾,故g(x)=不具有性质L


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （2009•黄冈模拟）定义在R上的偶函数y=f（x）满足：
    ①对x∈R都有f（x+6）=f（x）+f（3）
    ②f（-5）=-1；
    ③当x1，x2∈[0，3]且x1≠x2时，都有
    f(x1)-f(x2)x1-x2
    ＞0则
    （1）f（2009）=
    -1
    -1
    ；
    （2）若方程f（x）=0在区间[a，6-a]上恰有3个不同实根，实数a的取值范围是
    （-9，-3]
    （-9，-3]
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2003•北京）设y=f（x）是定义在区间[-1，1]上的函数，且满足条件：（i）f（-1）=f（1）=0；（ii）对任意的u，v∈[-1，1]，都有|f（u）-f（v）|≤|u-v|．
    （Ⅰ）证明：对任意的x∈[-1，1]，都有x-1≤f（x）≤1-x；
    （Ⅱ）判断函数g(x)=
    1+x，x∈[-1，0)
    1-x，x∈[0，1]
    是否满足题设条件；
    （Ⅲ）在区间[-1，1]上是否存在满足题设条件的函数y=f（x），且使得对任意的u，v∈[-1，1]，都有|f（u）-f（v）|=u-v．
    若存在，请举一例：若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年江西省高三上学期第三次月考数学文卷 题型：解答题

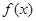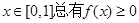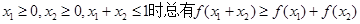    （12分）对定义在[0, 1]上并且满足下列两个条件的函数称为G函数。①对任意的，②成立。已知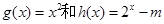是定义在[0, 1]上的函数。

    （1）问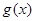是否为G函数，说明理由；

    （2）若是G函数，求实数m取值的范围。

     

    查看答案和解析>>

    科目：高中数学 来源：北京 题型：解答题

    设y=f（x）是定义在区间[-1，1]上的函数，且满足条件：（i）f（-1）=f（1）=0；（ii）对任意的u，v∈[-1，1]，都有|f（u）-f（v）|≤|u-v|．
    （Ⅰ）证明：对任意的x∈[-1，1]，都有x-1≤f（x）≤1-x；
    （Ⅱ）判断函数g(x)=
    1+x，x∈[-1，0)
    1-x，x∈[0，1]
    是否满足题设条件；
    （Ⅲ）在区间[-1，1]上是否存在满足题设条件的函数y=f（x），且使得对任意的u，v∈[-1，1]，都有|f（u）-f（v）|=u-v．
    若存在，请举一例：若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案