
已知双曲线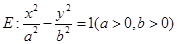 的离心率为e,左、右两焦点分别为F1、F2,焦距为
的离心率为e,左、右两焦点分别为F1、F2,焦距为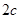 ,抛物线C以F2为顶点,F1为焦点,点P为抛物线与双曲线右支上的一个交点,若a|PF2|+c|PF1|=8a2,则e的值为 ( )
,抛物线C以F2为顶点,F1为焦点,点P为抛物线与双曲线右支上的一个交点,若a|PF2|+c|PF1|=8a2,则e的值为 ( )
| A. | B.3 | C. | D. |
A
解析考点:圆锥曲线的共同特征.
分析:作出图象,结合图象知抛物线准线的方程为x=3c,根据抛物线的定义可得|PF1|=|PR|=3c-x0,根据双曲线的第二定义可得 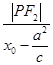 =e,由已知a|PF2|+c|PF1|=8a2,可得e= .
=e,由已知a|PF2|+c|PF1|=8a2,可得e= .
解:如右图所示,设点P的坐标为(x0,y0),由抛物线以F2为顶点,F1为焦点,可得其准线的方程为x=3c,
根据抛物线的定义可得|PF1|=|PR|=3c-x0,又由点P为双曲线上的点,
根据双曲线的第二定义可得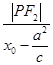 =e,即得|PF2|=ex0-a,
=e,即得|PF2|=ex0-a,
由已知a|PF2|+c|PF1|=8a2,可得-a2+3c2=8a2,即e2=3,由e>1可得e=,
故选A.


 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案科目:高中数学 来源: 题型:单选题
过抛物线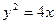 的焦点作一条直线与抛物线相交于A、B两点,它们的横坐标之
的焦点作一条直线与抛物线相交于A、B两点,它们的横坐标之 和等于5,则这样的直线 ( )
和等于5,则这样的直线 ( )
A.有且仅有一条 B.有且仅有两条 C.有无穷多条 D.不存在
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com