
【题目】已知函数f(x)=2cos2ωx+2sinωxcosωx(ω>0)的最小正周期为π.
(Ⅰ)求f(![]() )的值;
)的值;
(Ⅱ)求函数f(x)的单调递增区间.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)利用正弦、余弦的二倍角公式及辅助角公式化简函数的解析式,再利用正弦函数的周期性求得的![]() 值,进而可得函数的解析式;(2)利用正弦函数的单调性,解不等式
值,进而可得函数的解析式;(2)利用正弦函数的单调性,解不等式![]() 可求得函数
可求得函数![]() 的单调递增区间.
的单调递增区间.
试题解析:(Ⅰ)由题得,
f(x)=2cos2ωx+2sinωxcosωx=cos2ωx+sin2ωx+1=![]() sin(2ωx+
sin(2ωx+![]() )+1,
)+1,
因为f(x)的最小正周期为π,所以![]() =π,解得ω=1,
=π,解得ω=1,
所以f(x)=![]() sin(2x+
sin(2x+![]() )+1.
)+1.
则f(![]() )=
)=![]() sin(
sin(![]() +
+![]() )+1=
)+1=![]() (sin
(sin![]() cos
cos![]() +cos
+cos![]() sin
sin![]() )+1=
)+1=![]() .
.
(Ⅱ)由2kπ﹣![]() ≤2x+
≤2x+![]() ≤2kπ+
≤2kπ+![]()
![]() ,得 kπ﹣
,得 kπ﹣![]() ≤x≤kπ+
≤x≤kπ+![]()
![]() ,
,
所以函数f(x)的单调递增区间为[kπ﹣![]() ,kπ+
,kπ+![]() ]
]![]() .
.


 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源: 题型:
【题目】平面直角坐标系xOy中,已知F1、F2分别是椭圆C:![]() +
+![]() =1(a>b>0)的左、右焦点,且右焦点F2的坐标为(
=1(a>b>0)的左、右焦点,且右焦点F2的坐标为(![]() ,0),点(
,0),点(![]() ,
,![]() )在椭圆C上.
)在椭圆C上.
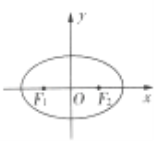
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)在椭圆C上任取一点P,点Q在PO的延长线上,且![]() =2.
=2.
(1)当点P在椭圆C上运动时,求点Q形成的轨迹E的方程;
(2)若过点P的直线l:y=x+m交(1)中的曲线E于A,B两点,求△ABQ面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直三棱柱ABC-A1B1C1中,AB=AA1,∠CAB=![]() .
.

(1)证明:CB1⊥BA1;
(2)已知AB=2,BC=![]() ,求三棱锥C1-ABA1的体积.
,求三棱锥C1-ABA1的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图(1)所示,在直角梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 与
与![]() 的交点.将△
的交点.将△![]() 沿
沿![]() 折起到△
折起到△![]() 的位置,如图(2)所示.
的位置,如图(2)所示.
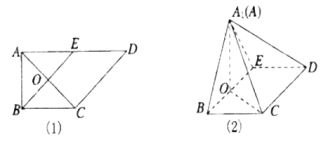
(1)证明:![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家之一,城市缺水问题较为突出,某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准![]() (吨),一位居民的月用水量不超过
(吨),一位居民的月用水量不超过![]() 的部分按平价收费,超出
的部分按平价收费,超出![]() 的部分按议价收费,为了了解居民用水情况,通过抽祥,获得了某年
的部分按议价收费,为了了解居民用水情况,通过抽祥,获得了某年![]() 位居民毎人的月均用水量(单位:吨),将数据按照
位居民毎人的月均用水量(单位:吨),将数据按照![]() 分成
分成![]() 组,制成了如图所示的频率分布直方图.
组,制成了如图所示的频率分布直方图.
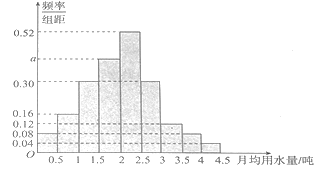
(1)求直方图中![]() 的值;
的值;
(2)若该市有![]() 万居民,估计全市居民中月均用水量不低于
万居民,估计全市居民中月均用水量不低于![]() 吨的人数,并说明理由;
吨的人数,并说明理由;
(3)若该市政府希望使![]() 的居民每月的用水量不超过标准
的居民每月的用水量不超过标准![]() (吨),估计
(吨),估计![]() 的值(精确到
的值(精确到![]() ),并说明理由.
),并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三国魏人刘徽,自撰《海岛算经》,专论测高望远.其中有一题:今有望海岛,立两表齐,高三丈,前後相去千步,令後表与前表相直。从前表却行一百二十三步,人目著地取望岛峰,与表末参合。从後表却行百二十七步,人目著地取望岛峰,亦与表末参合。问岛高及去表各几何?翻译如下:要测量海岛上一座山峰![]() 的高度
的高度![]() ,立两根高三丈的标杆
,立两根高三丈的标杆![]() 和
和![]() ,前后两竿相距
,前后两竿相距![]() 步,使后标杆杆脚
步,使后标杆杆脚![]() 与前标杆杆脚
与前标杆杆脚![]() 与山峰脚
与山峰脚![]() 在同一直线上,从前标杆杆脚
在同一直线上,从前标杆杆脚![]() 退行
退行![]() 步到
步到![]() ,人眼著地观测到岛峰,
,人眼著地观测到岛峰,![]() 、
、![]() 、
、![]() 、三点共线,从后标杆杆脚
、三点共线,从后标杆杆脚![]() 退行
退行![]() 步到
步到![]() ,人眼著地观测到岛峰,
,人眼著地观测到岛峰,![]() 、
、![]() 、
、![]() 三点也共线,则山峰的高度
三点也共线,则山峰的高度![]() __________步.(古制
__________步.(古制![]() 步
步![]() 尺,
尺,![]() 里
里![]() 丈
丈![]() 尺
尺![]() 步)
步)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com