【题目】有
、
、
、
四位贵宾，应分别对应坐在
、
、
、
四个席位上，现在这四人均未留意，在四个席位上随便就座.
（1）求这四人恰好都坐在自己席位上的概率；
（2）求这四人恰好都没坐在自己席位上的概率；
（3）求这四人恰好有
位坐在自己席位上的概率.
【答案】（1）
；（2）
；（3）
.
【解析】
以
分别表示
、
、
、
四位贵宾分别对应坐在
、
、
、
四个席位上，列举出所有的基本事件.
（1）列举出事件“这四人恰好都坐在自己席位上”所包含的基本事件，并利用古典概型的概率公式计算出该事件的概率；
（2）列举出事件“这四人恰好都没坐在自己席位上” 所包含的基本事件，并利用古典概型的概率公式计算出该事件的概率；
（3）列举出事件“这四人恰好有
位坐在自己席位上”所包含的基本事件，并利用古典概型的概率公式计算出该事件的概率.
以分别表示、、、四位贵宾分别对应坐在、、、四个席位上，所有的基本事件有：、
、
、
、
、
、
、
、
、
、
、
、
、
、
、
、
、
、
、
、
、
、
、
，共
个基本事件.
（1）事件“这四人恰好都坐在自己席位上”所包含的基本事件为：，因此所求概率为；
（2）事件“这四人恰好都没坐在自己席位上”所包含的基本事件有：、、、、、、、、，共
个基本事件，因此，所求概率为
；
（3）事件“这四人恰好有位坐在自己席位上”所包含的基本事件有：、、、、、、、，共
个基本事件，因此，所求概率为
.
名校课堂系列答案科目：高中数学 来源： 题型：
【题目】已知a＞0，b＞0，函数f（x）＝｜x＋a｜＋｜2x－b｜的最小值为1．
（1）证明：2a＋b＝2；
（2）若a＋2b≥tab恒成立，求实数t的最大值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下面是追踪调查200个某种电子元件寿命（单位:
)频率分布直方图，如图：
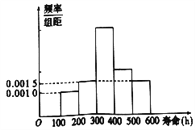
其中300-400、400-500两组数据丢失，下面四个说法中有且只有一个与原数据相符，这个说法是( )
①寿命在300-400的频数是90；
②寿命在400-500的矩形的面积是0.2；
③用频率分布直方图估计电子元件的平均寿命为：
④寿命超过
的频率为0.3
A. ① B. ② C. ③ D. ④
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下列随机事件：
①某射手射击一次，可能命中
环，
环，
环，
，
环；
②一个小组有男生
人，女生
人，从中任选人进行活动汇报；
③一只使用中的灯泡寿命长短；
④抛出一枚质地均匀的硬币，观察其出现正面或反面的情况；
⑤中秋节前夕，某市有关部门调查辖区内某品牌的月饼质量，给该品牌月饼评“优”或“差”.
这些事件中，属于古典概型的是________.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】若方程
所表示的曲线为C，给出下列四个命题：
①若C为椭圆，则
；
②若C为双曲线，则
或
；
③曲线C不可能是圆；
④若
，曲线C为椭圆，且焦点坐标为
；
⑤若，曲线C为双曲线，且虚半轴长为
．
其中真命题的序号为____________.（把所有正确命题的序号都填在横线上）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在古代，直角三角形中较短的直角边称为“勾”,较长的直角边称为“股”，斜边称为“弦”.三国时期吴国数学家赵爽用“弦图”( 如图) 证明了勾股定理，证明方法叙述为:“按弦图,又可以勾股相乘为朱实二，倍之为朱实四，以勾股之差自相乘为中黄实，加差实，亦成弦实.”这里的“实”可以理解为面积.这个证明过程体现的是这样一个等量关系:“两条直角边的乘积是两个全等直角三角形的面积的和(朱实二 )，4个全等的直角三角形的面积的和(朱实四) 加上中间小正方形的面积(黄实) 等于大正方形的面积(弦实)”. 若弦图中“弦实”为16，“朱实一”为
,现随机向弦图内投入一粒黄豆(大小忽略不计)，则其落入小正方形内的概率为( )
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知曲线C：x2－y2＝1及直线l：y＝kx－1.
(1)若l与C有两个不同的交点，求实数k的取值范围；
(2)若l与C交于A，B两点，O为坐标原点，且△AOB的面积为
，求实数k的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某公司有员工1000名，平均每人每年创造利润10万元．为了增加企业竞争力，决定优化产业结构，调整出
名员工从事第三产业，调整后他们平均每人每年创造利润为
万元（
），剩下的员工平均每人每年创造的利润可以提高
．
（1）若要保证剩余员工创造的年总利润不低于原来1000名员工创造的年总利润，则调整员工从事第三产业的人数应在什么范围？
（2）在（1）的条件下，若调整出的员工创造的年总利润始终不高于剩余员工创造的年总利润，求
的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】计划在某水库建一座至多安装3台发电机的水电站，过去50年的水文资料显示，水库年入流量
(年入流量：一年内上游来水与库区降水之和.单位：亿立方米）都在40以上.其中，不足80的年份有10年，不低于80且不超过120的年份有35年，超过120的年份有5年.将年入流量在以上三段的频率作为相应段的概率，并假设各年的年入流量相互独立.
（1）求未来4年中，至多1年的年入流量超过120的概率；
（2）水电站希望安装的发电机尽可能运行，但每年发电机最多可运行台数受年入流量
限制，并有如下关系:
年入流量 |
|
|
|
发电量最多可运行台数 | 1 | 2 | 3 |
若某台发电机运行，则该台年利润为5000万元；若某台发电机未运行，则该台年亏损800万元，欲使水电站年总利润的均值达到最大，应安装发电机多少台？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
