
【题目】已知直线![]() 、
、![]() 与平面
与平面![]() 、
、![]() 满足
满足![]() ,
,![]() ,
,![]() ,则下列命题中正确的是( )
,则下列命题中正确的是( )
A.![]() 是
是![]() 的充分不必要条件
的充分不必要条件
B.![]() 是
是![]() 的充要条件
的充要条件
C.设![]() ,则
,则![]() 是
是![]() 的必要不充分条件
的必要不充分条件
D.设![]() ,则
,则![]() 是
是![]() 的既不充分也不必要条件
的既不充分也不必要条件
【答案】C
【解析】
利用线面垂直、面面垂直的判定和性质定理,结合充分条件和必要条件的定义可判断出各选项中命题的正误.
对于A选项,如下图所示:
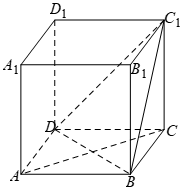
在正方体![]() 中,设
中,设![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,
平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
易知![]() 为正三角形,则
为正三角形,则![]() ,则
,则![]() ;
;
设![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() ,但平面
,但平面![]() 与平面
与平面![]() 不垂直,则
不垂直,则![]() .
.
所以,![]() 是
是![]() 的既不充分也不必要条件,A选项错误;
的既不充分也不必要条件,A选项错误;
对于B选项,如下图所示:

在正方体![]() 中,设
中,设![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,
![]() ,但平面
,但平面![]() 与平面
与平面![]() 不垂直,即
不垂直,即![]() ;
;
设![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,
平面![]() 平面
平面![]() ,但
,但![]() 与
与![]() 不垂直,即
不垂直,即![]() ,
,
所以,![]() 是
是![]() 的既不充分也不必要条件,B选项错误;
的既不充分也不必要条件,B选项错误;
对于C、D选项,如下图所示:

在正方体![]() 中,设
中,设![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,但
,但![]() 与
与![]() 不垂直,所以,若
不垂直,所以,若![]() ,
,![]() ;
;
若![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() .
.
所以,若![]() ,则
,则![]() 是
是![]() 的必要不充分条件,C选项正确,D选项错误.
的必要不充分条件,C选项正确,D选项错误.
故选:C.


 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源: 题型:
【题目】设三棱锥![]() 的每个顶点都在球
的每个顶点都在球![]() 的球面上,
的球面上,![]() 是面积为
是面积为![]() 的等边三角形,
的等边三角形,![]() ,
,![]() ,且平面
,且平面![]() 平面
平面![]() .
.
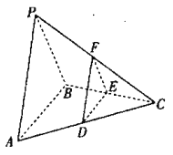
(1)确定![]() 的位置(需要说明理由),并证明:平面
的位置(需要说明理由),并证明:平面![]() 平面
平面![]() .
.
(2)与侧面![]() 平行的平面
平行的平面![]() 与棱
与棱![]() ,
,![]() ,
,![]() 分别交于
分别交于![]() ,
,![]() ,
,![]() ,求四面体
,求四面体![]() 的体积的最大值.
的体积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆柱![]() 底面半径为1,高为
底面半径为1,高为![]() ,
,![]() 是圆柱的一个轴截面,动点
是圆柱的一个轴截面,动点![]() 从点
从点![]() 出发沿着圆柱的侧面到达点
出发沿着圆柱的侧面到达点![]() ,其距离最短时在侧面留下的曲线
,其距离最短时在侧面留下的曲线![]() 如图所示.将轴截面
如图所示.将轴截面![]() 绕着轴
绕着轴![]() 逆时针旋转
逆时针旋转![]() 后,边
后,边![]() 与曲线
与曲线![]() 相交于点
相交于点![]() .
.
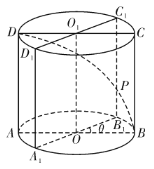
(1)求曲线![]() 的长度;
的长度;
(2)当![]() 时,求点
时,求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() ,以
,以![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 在曲线
在曲线![]() 上,直线
上,直线![]() 交曲线
交曲线![]() 于点
于点![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国仓储指数是反映仓储行业经营和国内市场主要商品供求状况与变化趋势的一套指数体系.如图所示的折线图是2017年和2018年的中国仓储指数走势情况.根据该折线图,下列结论中不正确的是( )

A. 2018年1月至4月的仓储指数比2017年同期波动性更大
B. 2017年、2018年的最大仓储指数都出现在4月份
C. 2018年全年仓储指数平均值明显低于2017年
D. 2018年各月仓储指数的中位数与2017年各月仓储指数中位数差异明显
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以原点
为参数).以原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,且直线
,且直线![]() 与曲线
与曲线![]() 交于
交于![]() 、
、![]() 两点.
两点.
(1)求实数![]() 的取值范围;
的取值范围;
(2)若![]() ,点
,点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() (
(![]() 为自然对数的底)。
为自然对数的底)。
(Ⅰ)求函数![]() 的单调区间;
的单调区间;
(Ⅱ)若存在均属于区间![]() 的
的![]() ,
,![]() ,且
,且![]() ,使
,使![]() ,证明:
,证明:![]() ;
;
(Ⅲ)对于函数![]() 与
与![]() 定义域内的任意实数
定义域内的任意实数![]() ,若存在常数
,若存在常数![]() ,
,![]() ,使得
,使得![]() 和
和![]() 都成立,则称直线
都成立,则称直线![]() 为函数
为函数![]() 与
与![]() 的分界线。试探究当
的分界线。试探究当![]() 时,函数
时,函数![]() 与
与![]() 是否存在“分界线”?若存在,请给予证明,并求出
是否存在“分界线”?若存在,请给予证明,并求出![]() ,
,![]() 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com