
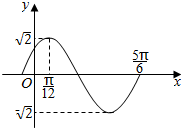
 函数f(x)=Asin(ωx+ϕ)$(A>0,ω>0,|φ|<\frac{π}{2})$的部分图象如图所示.
函数f(x)=Asin(ωx+ϕ)$(A>0,ω>0,|φ|<\frac{π}{2})$的部分图象如图所示.分析 (1)由题意和图象可得A值,由周期公式可得ω,代入点($\frac{π}{12}$,$\sqrt{2}$)结合角的范围可得;
(2)解不等式2kπ-$\frac{π}{2}$≤2x+$\frac{π}{3}$≤2kπ+$\frac{π}{2}$可得;
(3)原不等式可化为-$\sqrt{2}$≤$\sqrt{2}$sin(2x+$\frac{π}{3}$)≤1,结合函数的图象可得.
解答 解:(1)由题意和图象可得A=$\sqrt{2}$,$\frac{3}{4}$•$\frac{2π}{ω}$=$\frac{5π}{6}$-$\frac{π}{12}$,解得ω=2,
∴f(x)=$\sqrt{2}$sin(2x+ϕ),代入点($\frac{π}{12}$,$\sqrt{2}$)可得$\sqrt{2}$=$\sqrt{2}$sin($\frac{π}{6}$+ϕ),
∴$\frac{π}{6}$+ϕ=2kπ+$\frac{π}{2}$,解得ϕ=2kπ+$\frac{π}{3}$,结合|ϕ|<$\frac{π}{2}$可得ϕ=$\frac{π}{3}$,
∴f(x)=$\sqrt{2}$sin(2x+$\frac{π}{3}$);
(2)由2kπ-$\frac{π}{2}$≤2x+$\frac{π}{3}$≤2kπ+$\frac{π}{2}$可解得kπ-$\frac{5π}{12}$≤x≤kπ+$\frac{π}{12}$,
∴函数f(x)的单调递增区间为:[kπ-$\frac{5π}{12}$,kπ+$\frac{π}{12}$](k∈Z);
(3)不等式-$\sqrt{2}$≤f(x)≤1可化为-$\sqrt{2}$≤$\sqrt{2}$sin(2x+$\frac{π}{3}$)≤1,
变形可得-1≤sin(2x+$\frac{π}{3}$)≤$\frac{\sqrt{2}}{2}$,故2kπ+$\frac{3π}{4}$≤2x+$\frac{π}{3}$≤2kπ+$\frac{9π}{4}$,
解得kπ+$\frac{5π}{24}$≤x≤kπ+$\frac{23π}{24}$,k∈Z
∴不等式-$\sqrt{2}$≤f(x)≤1的解集为[kπ+$\frac{5π}{24}$,kπ+$\frac{23π}{24}$]k∈Z.
点评 本题考查三角函数的故选和性质,涉及单调性和三角函数不等式的解集,属中档题.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | (-2,-2) | B. | (2,2) | C. | (-2,2) | D. | (2,-2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 株洲市某中学利用周末组织教职员工进行了一次秋季登石峰山健身的活动,有N人参加,现将所有参加人员按年龄情况分为[20,25),[25,30),[30,35],[35,40),[40,45),[45,50),[50,55)等七组,其频率分布直方图如图所示.已知[35,40)之间的参加者有8人.
株洲市某中学利用周末组织教职员工进行了一次秋季登石峰山健身的活动,有N人参加,现将所有参加人员按年龄情况分为[20,25),[25,30),[30,35],[35,40),[40,45),[45,50),[50,55)等七组,其频率分布直方图如图所示.已知[35,40)之间的参加者有8人.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 语句“x>0”是命题 | |
| B. | 若命题p为真命题,命题q为假命题,则p∨q为假命题 | |
| C. | 若命题p:?x∈R,x2+1≥0,则$?p:?{x_0}∈R,x_0^2+1≥0$ | |
| D. | 若一个命题的逆命题为假,则它的否命题一定为假 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{6}}}{3}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com