
【题目】已知二次函数![]() .
.
(1)若![]() 是
是![]() 的两个不同零点,是否存在实数
的两个不同零点,是否存在实数![]() ,使
,使![]() 成立?若存在,求
成立?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(2)设![]() ,函数
,函数 ,存在
,存在![]() 个零点.
个零点.
(i)求![]() 的取值范围;
的取值范围;
(ii)设![]() 分别是这
分别是这![]() 个零点中的最小值与最大值,求
个零点中的最小值与最大值,求![]() 的最大值.
的最大值.
【答案】(1) 不存在.理由见解析;
(2) (i) ![]() (ii)
(ii) ![]()
【解析】
(1) .假设存在实数![]() 满足题意,由韦达定理可得:
满足题意,由韦达定理可得:![]()
![]() ,解得
,解得![]() ,又
,又![]() ,即
,即![]() ,综合可得假设不成立;
,综合可得假设不成立;
(2) (i)作出函数![]() 的图象,观察图像即可求出
的图象,观察图像即可求出![]() 的取值范围;
的取值范围;
(ii)设直线![]() 与此图象的最左边和最右边的交点分别为
与此图象的最左边和最右边的交点分别为![]() .即
.即![]() ,因为
,因为![]()
![]() ,代入运算可得解.
,代入运算可得解.
解:(1)依题意可知,![]() .假设存在实数
.假设存在实数![]() ,使
,使![]() 成立.
成立.
因为![]() 有两个不同零点,.
有两个不同零点,.
所以![]() ,解得
,解得![]() .
.
由韦达定理得![]()
所以![]()
![]()
解得![]() ,而
,而![]() ,故不存在.
,故不存在.
(2)因为![]() ,设
,设![]() ,则
,则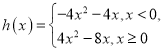 ,
,
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
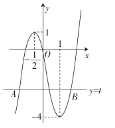
(i)作出函数![]() 的图象,如图所示,所以
的图象,如图所示,所以![]() .
.
(ii)设直线![]() 与此图象的最左边和最右边的交点分别为
与此图象的最左边和最右边的交点分别为![]() .
.
由![]() ,得
,得![]()
由![]() ,得
,得![]()
所以![]()
因为![]()
![]() ,
,
所以当![]() 时,
时,![]() 取得最大值
取得最大值![]() .
.
故![]() 的最大值为
的最大值为![]() .
.


 高中必刷题系列答案
高中必刷题系列答案科目:高中数学 来源: 题型:
【题目】某地电影院为了了解当地影迷对快要上映的一部电影的票价的看法,进行了一次调研,得到了票价x(单位:元)与渴望观影人数y(单位:万人)的结果如下表:
x(单位:元) | 30 | 40 | 50 | 60 |
y(单位:万人) | 4.5 | 4 | 3 | 2.5 |
(1)若y与x具有较强的相关关系,试分析y与x之间是正相关还是负相关;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程;
(3)根据(2)中求出的线性回归方程,预测票价定为多少元时,能获得最大票房收入.
参考公式: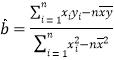 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究学生的数学核素养与抽象(能力指标![]() )、推理(能力指标
)、推理(能力指标![]() )、建模(能力指标
)、建模(能力指标![]() )的相关性,并将它们各自量化为1、2、3三个等级,再用综合指标
)的相关性,并将它们各自量化为1、2、3三个等级,再用综合指标![]() 的值评定学生的数学核心素养,若
的值评定学生的数学核心素养,若![]() ,则数学核心素养为一级;若
,则数学核心素养为一级;若![]() ,则数学核心素养为二级;若
,则数学核心素养为二级;若![]() ,则数学核心素养为三级,为了了解某校学生的数学核素养,调查人员随机访问了某校10名学生,得到如下:
,则数学核心素养为三级,为了了解某校学生的数学核素养,调查人员随机访问了某校10名学生,得到如下:

(1)在这10名学生中任取两人,求这两人的建模能力指标相同的概率;
(2)从数学核心素养等级是一级的学生中任取一人,其综合指标为![]() ,从数学核心素养等级不是一级的学生中任取一人,其综合指标为
,从数学核心素养等级不是一级的学生中任取一人,其综合指标为![]() ,记随机变量
,记随机变量![]() ,求随机变量
,求随机变量![]() 的分布列及其数学期望.
的分布列及其数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量![]() =(2sinx,-1),
=(2sinx,-1),![]() ,函数f(x)=
,函数f(x)=![]() .
.
(1)求函数f(x)的对称中心;
(2)设△ABC的内角A,B,C所对的边为a,b,c,且a2=bc,求f(A)的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】向50名学生调查对A、B两事件的态度,有如下结果:赞成A的人数是全体的五分之三,其余的不赞成,赞成B的比赞成A的多3人,其余的不赞成;另外,对A、B都不赞成的学生数比对A、B都赞成的学生数的三分之一多1人. 问对A、B都赞成的学生有____________人
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学用“五点法”画函数![]() 在某一个周期内的图象时,列表并填入了部分数据,如下表:
在某一个周期内的图象时,列表并填入了部分数据,如下表:
| 0 |
|
|
|
|
|
|
| |||
| 0 | 2 | 0 | 0 |
(1)请将上表数据补充完整;函数![]() 的解析式为
的解析式为![]() = (直接写出结果即可);
= (直接写出结果即可);
(2)求函数![]() 的单调递增区间;
的单调递增区间;
(3)求函数![]() 在区间
在区间![]() 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com