
【题目】已知函数![]() ,
,![]() 为自然对数的底数(
为自然对数的底数(![]() ).
).
(1)当![]() 时,求
时,求![]() 的定义域;
的定义域;
(2)若![]() ,讨论
,讨论![]() 时,
时,![]() 的值域.
的值域.
【答案】(1)![]() (2)答案不唯一,见解析
(2)答案不唯一,见解析
【解析】
(1)由题求解![]() ,因式分解求解即可.
,因式分解求解即可.
(2) 设![]() 求得
求得![]() ,再利用定义证明
,再利用定义证明![]() 在
在![]() 内为减函数,在
内为减函数,在![]() 内为增函数,进而分类讨论利用函数的单调性分析最值与值域即可.
内为增函数,进而分类讨论利用函数的单调性分析最值与值域即可.
(1)要使![]() 有意义
有意义
必须且只需![]()
即![]()
![]()
![]()
![]() 的定义域为
的定义域为![]() ;
;
(2)![]()
设![]()
![]()
![]()
下面证明函数![]() 在
在![]() 内为减函数,在
内为减函数,在![]() 内为增函数
内为增函数
设![]() ,
,
![]()
![]()
![]()
![]()
![]() 在
在![]() 内为增函数;
内为增函数;
为增函数同理可证,![]() 在
在![]() 内为减函数.
内为减函数.
当![]() ,即
,即![]() 时(等号必须取),
时(等号必须取),![]() 在
在![]() 上为减函数,
上为减函数,
![]()
![]() 的值域为
的值域为![]() .
.
![]() 时,
时,![]() 的值域为
的值域为![]()
当![]() 时(不能等于9),
时(不能等于9),![]() ,
,![]() 在
在![]() 上为减函数,在
上为减函数,在![]() 上为增函数,
上为增函数,
![]() ,
,![]() 为
为![]() 与
与![]() 中的较大者,
中的较大者,
![]() ,
,
当![]() 时(可以取等于3),
时(可以取等于3),![]() ,
,
![]() 的值域为
的值域为![]() ,
,![]() 的值域为
的值域为![]()
当![]() 时(可以在上面取等于3),
时(可以在上面取等于3),![]() ,
,
![]() 的值域为
的值域为![]() ,
,![]() 的值域为
的值域为![]()
综上所述,当![]() 时(可以取等于3),
时(可以取等于3),![]() 的值域为
的值域为![]() ;
;
当![]() 时(可以在上面取等于3),
时(可以在上面取等于3),![]() 的值域为
的值域为![]()
当![]() 时,
时,![]() 的值域为
的值域为![]()


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源: 题型:
【题目】甲、乙两人2013-2017这五年的年度体检的血压值的折线图如图所示.
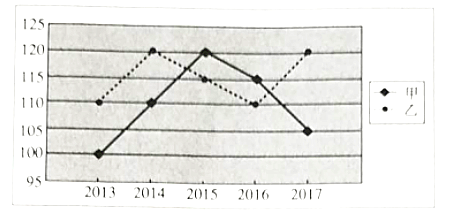
(1)根据散点图,直接判断甲、乙这五年年度体检的血压值谁的波动更大,并求波动更大者的方差;
(2)根据乙这五年年度体检血压值的数据,求年度体检血压值![]() 关于年份
关于年份![]() 的线性回归方程,并据此估计乙在2018年年度体检的血压值.
的线性回归方程,并据此估计乙在2018年年度体检的血压值.
(附: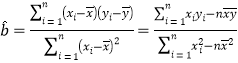 ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年初,我国突发新冠肺炎疫情.面对“突发灾难”,举国上下心,继解放军医疗队于除夕夜飞抵武汉,各省医疗队也陆续增援,纷纷投身疫情防控与病人救治之中.为分担“逆行者”的后顾之忧,某大学学生志愿者团队开展“爱心辅学”活动,为抗疫前线工作者子女在线辅导功课.现随机安排甲、乙、丙3名志愿者为某学生辅导数学、物理、化学、生物4门学科,每名志愿者至少辅导1门学科,每门学科由1名志愿者辅导,则数学学科恰好由甲辅导的概率为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有女子善织,日益功,疾,初日织五尺,今一月织七匹三丈(1匹=![]() 尺,一丈=
尺,一丈=![]() 尺),问日益几何?”其意思为:“有一女子擅长织布,每天比前一天更加用功,织布的速度也越来越快,从第二天起,每天比前一天多织相同量的布,第一天织
尺),问日益几何?”其意思为:“有一女子擅长织布,每天比前一天更加用功,织布的速度也越来越快,从第二天起,每天比前一天多织相同量的布,第一天织![]() 尺,一月织了七匹三丈,问每天增加多少尺布?”若这一个月有
尺,一月织了七匹三丈,问每天增加多少尺布?”若这一个月有![]() 天,记该女子一个月中的第
天,记该女子一个月中的第![]() 天所织布的尺数为
天所织布的尺数为![]() ,则
,则![]() 的值为( )
的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,点
,点![]() ,直线
,直线![]() .
.
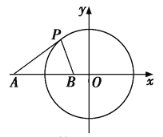
(1)求与直线l垂直,且与圆C相切的直线方程;
(2)在x轴上是否存在定点B(不同于点A),使得对于圆C上任一点P,![]() 为常数?若存在,试求这个常数值及所有满足条件的点B的坐标;若不存在,请说明理由.
为常数?若存在,试求这个常数值及所有满足条件的点B的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十九大以来,某贫困地区扶贫办积极贯彻落实国家精准扶贫的政策要求,带领广大农村地区人民群众脱贫奔小康.经过不懈的奋力拼搏,新农村建设取得巨大进步,农民收入也逐年增加.为了更好的制定2019年关于加快提升农民年收入力争早日脱贫的工作计划,该地扶贫办统计了2018年50位农民的年收入并制成如下频率分布直方图:
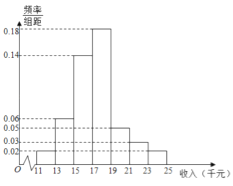
附:参考数据与公式 ![]() ,若
,若 ![]() ,则①
,则① ![]() ;②
;② ![]() ;③
;③ ![]() .
.
(1)根据频率分布直方图估计50位农民的年平均收入![]() (单位:千元)(同一组数据用该组数据区间的中点值表示);
(单位:千元)(同一组数据用该组数据区间的中点值表示);
(2)由频率分布直方图可以认为该贫困地区农民年收入 X 服从正态分布 ![]() ,其中
,其中![]() 近似为年平均收入
近似为年平均收入![]() 近似为样本方差
近似为样本方差![]() ,经计算得:
,经计算得:![]() ,利用该正态分布,求:
,利用该正态分布,求:
(i)在2019年脱贫攻坚工作中,若使该地区约有占总农民人数的84.14%的农民的年收入高于扶贫办制定的最低年收入标准,则最低年收入大约为多少千元?
(ii)为了调研“精准扶贫,不落一人”的政策要求落实情况,扶贫办随机走访了1000位农民.若每个农民的年收入相互独立,问:这1000位农民中的年收入不少于12.14千元的人数最有可能是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com