
| P��K2��k0�� | 0.100 | 0.050 | 0.010 |
| k0 | 6.635 | 7.879 | 10.828 |
���� ��1�����ù�ʽ�����K2�������ó����ۣ�
��2�������ȡ1��ѧ���ijɼ�����ѧ���������Ƴɼ�ǡ��һ������ĸ���Ϊ$p=\frac{200}{800}=\frac{1}{4}$��������X��B��4��$\frac{1}{4}$�������ɵó�X�ķֲ��м�����ѧ������
��� �⣺��1���г���2��2������Ϊ��
| ��ѧ�ɼ� | �����ɼ� | �ϼ� | |
| ���� | 200 | 120 | 320 |
| ������ | 600 | 680 | 1280 |
| �ϼ� | 800 | 800 | 1600 |
| X | 0 | 1 | 2 | 3 | 4 |
| p | $\frac{81}{256}$ | $\frac{27}{64}$ | $\frac{27}{128}$ | $\frac{3}{64}$ | $\frac{1}{256}$ |
���� ���⿼���˶����Լ���˼�롢����ֲ��м�����ѧ����������������������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
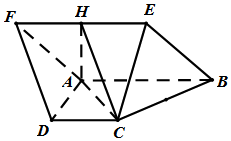 ��ͼ��ʾ������ABEF��ֱ������ABCD����BAD=��CDA=90�㣬��ABE=60�㣬AB=2AD=2CD=2��H��EF���е�
��ͼ��ʾ������ABEF��ֱ������ABCD����BAD=��CDA=90�㣬��ABE=60�㣬AB=2AD=2CD=2��H��EF���е��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $[\frac{1}{2}��2]$ | B�� | $[\frac{1}{3}��3]$ | C�� | $[\frac{3}{2}��3]$ | D�� | $[\frac{4}{3}��4]$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4 | B�� | 4.5 | C�� | 5 | D�� | 5.5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ģ��1 | B�� | ģ��2 | C�� | ģ��3 | D�� | ģ��4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
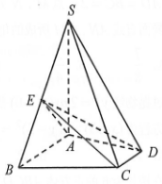 ��ͼ����֪����S-ABCD�У�SA��ƽ��ABCD����ABC=��BCD=90�㣬��SA=AB=BC=2CD=2��E�DZ�SB���е㣮
��ͼ����֪����S-ABCD�У�SA��ƽ��ABCD����ABC=��BCD=90�㣬��SA=AB=BC=2CD=2��E�DZ�SB���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com