
| A. | $\frac{5}{8}$ | B. | $\frac{5}{16}$ | C. | $\frac{4}{7}$ | D. | $\frac{5}{14}$ |
分析 根据题意,利用条件概率计算公式求出事件A发生的条件下事件B发生的概率即可.
解答 解:一个口袋中装有5个白球,3个红球,每次从袋中随机摸出一个球,不放回地摸2次,
A表示“第一次拿出的是白球”,B表示“第二次拿出的是白球”,
则P(A)=$\frac{5}{8}$,P(AB)=$\frac{5}{8}$×$\frac{4}{7}$=$\frac{5}{14}$;
在摸出的第一个是白球的条件下,摸出的第二个球是白球的概率是:
p(B|A)=$\frac{\frac{5}{14}}{\frac{5}{8}}$=$\frac{4}{7}$.
故选:C.
点评 本题考查了条件概率的计算问题,是基础题目.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{2}$ | B. | $\frac{8}{5}$ | C. | $\frac{5}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 6 | C. | 4 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
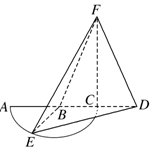 如图,以AC=2为直径的⊙B,点E为$\widehat{AC}$的中点,点D在直径AC延长线上,CD=1,FC⊥平面BED,FC=2.
如图,以AC=2为直径的⊙B,点E为$\widehat{AC}$的中点,点D在直径AC延长线上,CD=1,FC⊥平面BED,FC=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com