
 已知如图,△ABC和△DBC所在的平面互相垂直,且AB=BC=BD=1,∠ABC=∠DBC=120°
已知如图,△ABC和△DBC所在的平面互相垂直,且AB=BC=BD=1,∠ABC=∠DBC=120°分析 (1)在平面ABC内作AH⊥BC,H是垂足,连HD,则AH⊥平面BDC,HD⊥BC,由三垂线定理能证明AD⊥BC.
(2)在平面BDC内作HR⊥BD,连AR,则∠ARH是二面角A-BD-C的平面角的补角,由此能求出二面角A-BD-C的余弦值.
解答 (1)证明:在平面ABC内作AH⊥BC,H是垂足,连HD.
因为平面ABC⊥平面BDC.所以AH⊥平面BDC.
HD是AD在平面BDC的射影.依题设条件得HD⊥BC,
∴由三垂线定理得AD⊥BC.
(2)解:在平面BDC内作HR⊥BD,R是垂足,连AR.
HR是AR在平面BDC的射影,∴AR⊥BD,
∴∠ARH是二面角A-BD-C的平面角的补角,
设AB=a,得AH=$\frac{\sqrt{3}}{2}a$,HR=$\frac{\sqrt{3}}{2}$BH=$\frac{\sqrt{3}}{4}a$,
∴cos$∠ARH=\frac{RH}{AR}$=$\frac{\frac{\sqrt{3}a}{4}}{\sqrt{(\frac{\sqrt{3}}{2}a)^{2}+(\frac{\sqrt{3}}{4}a})^{2}}$=$\frac{\sqrt{5}}{5}$.
∴二面角A-BD-C的余弦值为$\frac{\sqrt{5}}{5}$.
点评 本题考查异面直线垂直的证明,考查二面角的余弦值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


科目:高中数学 来源:2015-2016学年江苏泰兴中学高二上学期期末数学(文)试卷(解析版) 题型:填空题
在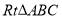 中,
中,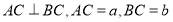 ,则
,则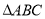 的外接圆半径
的外接圆半径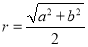 ;类比到空间,若三棱锥
;类比到空间,若三棱锥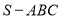 的三条侧棱
的三条侧棱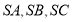 两两互相垂直,且长度分别为
两两互相垂直,且长度分别为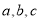 ,则三棱锥
,则三棱锥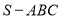 的外接球的半径
的外接球的半径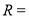 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
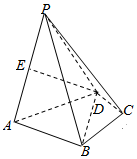 如图,在四棱锥P-ABCD中,△ABD是边长为2$\sqrt{3}$的正三角形,∠CBD=∠CDB=30°,E为棱PA的中点.
如图,在四棱锥P-ABCD中,△ABD是边长为2$\sqrt{3}$的正三角形,∠CBD=∠CDB=30°,E为棱PA的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=120°,AB=PC=2,AP=BP=$\sqrt{2}$.
如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=120°,AB=PC=2,AP=BP=$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 一个正方体削去一个角所几何体的三视图如图所示(图中三个四边形都是边长为2的正方形),若削去的几何体中原正方体的顶点到截面的距离为h,削去的几何体中内切球的半径为R,则$\frac{h}{R}$的值为( )
一个正方体削去一个角所几何体的三视图如图所示(图中三个四边形都是边长为2的正方形),若削去的几何体中原正方体的顶点到截面的距离为h,削去的几何体中内切球的半径为R,则$\frac{h}{R}$的值为( )| A. | $\frac{\sqrt{6}}{2}$ | B. | 2$\sqrt{3}$ | C. | 1+$\sqrt{3}$ | D. | $\frac{1+\sqrt{2}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
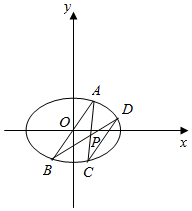 如图,在平面直角坐标系xOy中,已知椭圆E:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,点A(${\frac{1}{3}$,$\frac{2}{3}}$)在椭圆E上,射线AO与椭圆E的另一交点为B,点P(-4t,t)在椭圆E内部,射线AP,BP与椭圆E的另一交点分别为C,D.
如图,在平面直角坐标系xOy中,已知椭圆E:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,点A(${\frac{1}{3}$,$\frac{2}{3}}$)在椭圆E上,射线AO与椭圆E的另一交点为B,点P(-4t,t)在椭圆E内部,射线AP,BP与椭圆E的另一交点分别为C,D.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com