求一切实数p,使得三次方程5x3-5(p+1)x2+(71p-1)x+1=66p的三个根均为正整数.
【答案】
分析:因为5x
3-5(p+1)x
2+(71p-1)x+1=66p=(x-1)(5x
2-5px+66p-1)=0,所以使三次方程5x
3-5(p+1)x
2+(71p-1)x+1=66p的三个根均为正整数,只要考虑二次方程5x
2-5px+66p-1=0的两个根为正整数即可.
解答:解:x=1是方程的一个根.于是只要考虑二次方程5x
2-5px+66p-1=0的两个根为正整数即可.
设此二正整数根为u、v.则由韦达定理知,
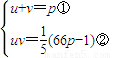
消去p,得5uv-66(u+v)=-1.同乘以5:5
2uv-5×66u-5×66v=-5.
∴(5u-66)(5v-66)=66
2-5=4351=19×229.由于u、v均为整数,故5u-66、5v-66为整数.
∴
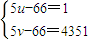
或

或
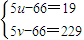
或

∴其中使u、v为正整数的,只有u=17,v=59这一组值.此时p=76.
点评:本题考查了函数零点与方程根的关系,考查了转化思想,解答此题的关键是把三次方程根的情况转化为二次方程根的情况,能够变抽象思维为形象思维,有助于把握数学问题的本质.

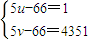

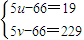



 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案