
分析 (1)化简函数f(x)的解析式,求出f(x)=0的x值,结合f(x)的图象可得不等式f(x)≤0的解集.
(2)由题意可得|x-2|+|x-$\frac{5}{2}$|≥-$\frac{m}{2}$恒成立,利用绝对值三角不等式求得|x-2|+|x-$\frac{5}{2}$|的最小值,可得实数m的取值范围.
解答  解:函数f(x)=|x-2|-|2x+5|=$\left\{\begin{array}{l}{x+7,x<-\frac{5}{2}}\\{-3x-3,-\frac{5}{2}≤x≤2}\\{-x-7,x>2}\end{array}\right.$,
解:函数f(x)=|x-2|-|2x+5|=$\left\{\begin{array}{l}{x+7,x<-\frac{5}{2}}\\{-3x-3,-\frac{5}{2}≤x≤2}\\{-x-7,x>2}\end{array}\right.$,
(1)令f(x)=|x-2|-|2x+5|=0,求得x=-7 或x=-1,结合f(x)的图象,
故不等式f(x)≤0的解集为{x|-7≤x≤-1}.
(2)若f(x)-3|x-2|≤m,对一切实数x均成立,
即:-2|x-2|-|2x+5|≤m恒成立;
即|x-2|+|x+$\frac{5}{2}$|≥-$\frac{m}{2}$恒成立;
y=|x-2|+|x+$\frac{5}{2}$|的图象为: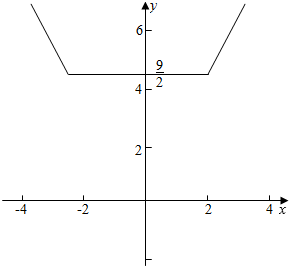
∴-$\frac{m}{2}$≤$\frac{9}{2}$;
所以m≥-9;
即m的取值范围为m≥-9.
点评 本题主要考查分段函数的应用,绝对值三角不等式的应用,绝对值不等式的解法,绝对值的意义,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
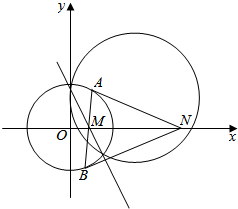 已知圆O:x2+y2=4和圆C:x2+y2-2x-y-2=0,记两圆的公共弦所在的直线为l.
已知圆O:x2+y2=4和圆C:x2+y2-2x-y-2=0,记两圆的公共弦所在的直线为l.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | S△AOC的最小值为$\frac{1}{2}$S | B. | SAOB的最小值为($\sqrt{2}$-1)S | ||
| C. | S△AOC+S△AOB的最大值为$\frac{1}{2}$S | D. | S△BOC的最大值为($\sqrt{2}$-1)S |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
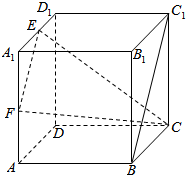 如图,在棱长为1的正方体ABCD-A1B1C1D1中,E,F分别是A1D1,A1A的中点.
如图,在棱长为1的正方体ABCD-A1B1C1D1中,E,F分别是A1D1,A1A的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,长方体ABCD-A1B1C1D1的底面边长均为1,侧棱AA1=2,M,N分别是A1C1,A1A的中点,
如图,长方体ABCD-A1B1C1D1的底面边长均为1,侧棱AA1=2,M,N分别是A1C1,A1A的中点,查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com