
【题目】若实数![]() 满足
满足![]() ,则称
,则称![]() 比
比![]() 接近
接近![]()
(1)若4比![]() 接近0,求
接近0,求![]() 的取值范围;
的取值范围;
(2)对于任意的两个不等正数![]() ,求证:
,求证:![]() 比
比![]() 接近
接近![]() ;
;
(3)若对于任意的非零实数![]() ,实数
,实数![]() 比
比![]() 接近
接近![]() ,求
,求![]() 的取值范围
的取值范围
【答案】(1)![]() ;(2)证明见解析;(3)
;(2)证明见解析;(3)![]()
【解析】
(1)由题意得:|x2﹣3x|>4,则x2﹣3x>4或x2﹣3x<﹣4,由此求得x的范围.
(2)根据![]() ,且
,且![]() ,化简|
,化简|![]() |﹣|a+b﹣2
|﹣|a+b﹣2![]() |的结果大于零,可得a+b比
|的结果大于零,可得a+b比![]() 接近
接近![]() .
.
(3)由题意![]() 对于x∈R,x≠0恒成立,分类讨论求得|x
对于x∈R,x≠0恒成立,分类讨论求得|x![]() 1|的最小值,可得|a+1|的范围,从而求得a的范围.
1|的最小值,可得|a+1|的范围,从而求得a的范围.
解:(1)由题意得:|x2﹣3x|>4,则x2﹣3x>4或x2﹣3x<﹣4,
由x2﹣3x>4,求得x>4或x<﹣1;由x2﹣3x<﹣4,求得x无解.
所以x取值范围为(﹣∞,﹣1)∪(4,+∞).
(2)因为a,b>0且a≠b,所以![]() ,且
,且![]() ,
,
所以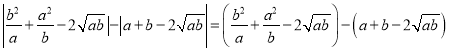
![]() ,
,
则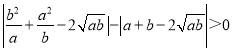 ,
,
即a+b比![]() 接近
接近![]() .
.
(3)由题意:![]() 对于x∈R,x≠0恒成立,
对于x∈R,x≠0恒成立,
当x>0时,![]() ,当x=2时等号成立,
,当x=2时等号成立,
当x<0时,则﹣x>0,![]() ,当x=﹣2时等号成立,所以
,当x=﹣2时等号成立,所以![]() ,则
,则![]() ,
,
综上![]() .
.
故由|a+1|<3,求得﹣4<a<2,即a取值范围为(﹣4,2).


科目:高中数学 来源: 题型:
【题目】为了解社会对学校办学质量的满意程度,某学校决定用分层抽样的方法从高中三个年级的家长委员会中共抽取![]() 人进行问卷调查,已知高一、高二、高三、的家长委员会分别有
人进行问卷调查,已知高一、高二、高三、的家长委员会分别有![]() 人,
人,![]() 人,
人,![]() 人.
人.
![]() 求从三个年级的家长委员会分别应抽到的家长人数;
求从三个年级的家长委员会分别应抽到的家长人数;
![]() 若从抽到的
若从抽到的![]() 人中随机抽取
人中随机抽取![]() 人进行调查结果的对比,求这
人进行调查结果的对比,求这![]() 人中至少有一人是高三学生家长的概率.
人中至少有一人是高三学生家长的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 与
与![]() 有相同的渐近线,且经过点
有相同的渐近线,且经过点![]() ,
,
(1)求双曲线![]() 的方程,并写出其离心率与渐近线方程;
的方程,并写出其离心率与渐近线方程;
(2)已知直线![]() 与双曲线
与双曲线![]() 交于不同的两点
交于不同的两点![]() ,且线段
,且线段![]() 的中点在圆
的中点在圆![]() 上,求实数
上,求实数![]() 的取值.
的取值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】商店出售茶壶和茶杯,茶壶定价每个20元,茶杯每个5元,该商店推出两种优惠办法:(1)买一个茶壶赠一个茶杯;(2)按总价的92%付款.
某顾客需购买茶壶4个,茶杯若干个(不少于4个),若购买茶杯数x个,付款y(元),分别建立两种优惠办法中y与x之间的函数关系式,并讨论该顾客买同样多的茶杯时,两种办法哪一种更优惠。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四大名著是中国文学史上的经典作品,是世界宝贵的文化遗产.某学校举行的“文学名著阅读月”活动中,甲、乙、丙、丁、戊五名同学相约去学校图书室借阅四大名著《红楼梦》、《三国演义》、《水浒传》、《西游记》(每种名著均有若干本),要求每人只借阅一本名著,每种名著均有人借阅,且甲只借阅《三国演义》,则不同的借阅方案种数为_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数集M满足条件:若![]() ,则
,则![]() .
.
(1)若![]() ,求集合M中一定存在的元素;
,求集合M中一定存在的元素;
(2)集合M内的元素能否只有一个?请说明理由;
(3)请写出集合M中的元素个数的所有可能值,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com