
【题目】如图,在四棱锥![]() 中,平面
中,平面![]() 平面
平面![]()
![]() ,点
,点![]() 分别为
分别为![]() 的中点.
的中点.
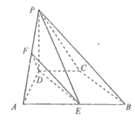
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
科目:高中数学 来源: 题型:
【题目】设满足以下两个条件的有穷数列![]() 为
为![]() 阶“期待数列”:①
阶“期待数列”:①![]() ;②
;②![]() .
.
(1)分别写出一个单调递增的3阶和4阶“期待数列”;
(2)若某2013阶“期待数列”是等差数列,求该数列的通项公式;
(3)记![]() 阶“期待数列”的前
阶“期待数列”的前![]() 项和为
项和为![]() ,试证:
,试证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的方程为
的方程为![]() ,过原点作斜率为
,过原点作斜率为![]() 的直线和曲线
的直线和曲线![]() 相交,另一个交点记为
相交,另一个交点记为![]() ,过
,过![]() 作斜率为
作斜率为![]() 的直线和曲线
的直线和曲线![]() 相交,另一个交点记为
相交,另一个交点记为![]() ,过
,过![]() 作斜率为
作斜率为![]() 的直线和曲线
的直线和曲线![]() 相交,另一个交点记为
相交,另一个交点记为![]() ,……,如此下去,一般地,过
,……,如此下去,一般地,过![]() 作斜率为
作斜率为![]() 的直线和曲线
的直线和曲线![]() 相交,另一个交点记为
相交,另一个交点记为![]() ,设点
,设点![]() .
.
(1)指出![]() ,并求
,并求![]() 与
与![]() 的关系式
的关系式![]() ;
;
(2)求![]() 的通项公式,并指出点列
的通项公式,并指出点列![]() ,
,![]() ,……,
,……,![]() ,……向哪一点无限接近?说明理由;
,……向哪一点无限接近?说明理由;
(3)令![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,设
,设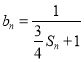 ,求所有可能的乘积
,求所有可能的乘积![]() 的和.
的和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若定义域均为D的三个函数f(x),g(x),h(x)满足条件:对任意x∈D,点(x,g(x)与点(x,h(x)都关于点(x,f(x)对称,则称h(x)是g(x)关于f(x)的“对称函数”.已知g(x)=![]() ,f(x)=2x+b,h(x)是g(x)关于f(x)的“对称函数”,且h(x)≥g(x)恒成立,则实数b的取值范围是_____.
,f(x)=2x+b,h(x)是g(x)关于f(x)的“对称函数”,且h(x)≥g(x)恒成立,则实数b的取值范围是_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学在一山坡![]() 处看对面山顶上的一座铁塔,如图所示,塔及所在的山崖可视为图中的竖线
处看对面山顶上的一座铁塔,如图所示,塔及所在的山崖可视为图中的竖线![]() ,塔高
,塔高![]() 为80米,山高
为80米,山高![]() 为220米,
为220米,![]() 为200米,图中所示的山坡可视为直线
为200米,图中所示的山坡可视为直线![]() 且点
且点![]() 在直线
在直线![]() 上,
上,![]() 与水平地面的夹角为
与水平地面的夹角为![]() ,
,![]() .
.

(1)求塔尖![]() 到山坡的距离;(精确到米)
到山坡的距离;(精确到米)
(2)问此同学(忽略身高)距离山崖的水平地面多高时,观看塔的视角![]() 最大?
最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com