
已知数列{an}和{bn}满足:a1=λ,an+1=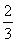 an+n-4,bn=(-1)n(an-3n+21),其中λ为实数,n为正整数.
an+n-4,bn=(-1)n(an-3n+21),其中λ为实数,n为正整数.
(1)对任意实数λ,证明:数列{an}不是等比数列;
(2)试判断数列{bn}是否为等比数列,并证明你的结论.
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:高中数学 来源:2014年高考数学(文)二轮复习真题感悟江苏专用常考问题2练习卷(解析版) 题型:填空题
已知e1,e2是夹角为 π的两个单位向量,a=e1-2e2,b=ke1+e2,若a·b=0,则k的值为________.
π的两个单位向量,a=e1-2e2,b=ke1+e2,若a·b=0,则k的值为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用阶段检测5练习卷(解析版) 题型:填空题
盒子里共有大小相同的3只白球,1只黑球.若从中随机摸出两只球,则它们颜色相同的概率是________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用阶段检测4练习卷(解析版) 题型:填空题
设圆C的圆心与双曲线 =1(a>0)的右焦点重合,且该圆与此双曲线的渐近线相切,若直线l:x-
=1(a>0)的右焦点重合,且该圆与此双曲线的渐近线相切,若直线l:x- y=0被圆C截得的弦长等于2,则a的值为________.
y=0被圆C截得的弦长等于2,则a的值为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用阶段检测3练习卷(解析版) 题型:解答题
已知数列{an}满足a1=a(a>0,a∈N*),a1+a2+…+an-pan+1=0(p≠0,p≠-1,n∈N*).
(1)求数列{an}的通项公式an;
(2)若对每一个正整数k,若将ak+1,ak+2,ak+3按从小到大的顺序排列后,此三项均能构成等差数列,且公差为dk.①求p的值及对应的数列{dk}.
②记Sk为数列{dk}的前k项和,问是否存在a,使得Sk<30对任意正整数k恒成立?若存在,求出a的最大值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用阶段检测3练习卷(解析版) 题型:填空题
Sn是等比数列{an}的前n项和,a1= ,9S3=S6,设Tn=a1a2a3…an,则使Tn取最小值的n值为________.
,9S3=S6,设Tn=a1a2a3…an,则使Tn取最小值的n值为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用阶段检测3练习卷(解析版) 题型:填空题
设公比为q(q>0)的等比数列{an}的前n项和为Sn,若S2=3a2+2,S4=3a4+2,则q=________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用阶段检测2练习卷(解析版) 题型:填空题
若M为△ABC所在平面内一点,且满足(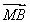 -
-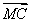 )·(
)·(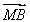 +
+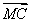 -2
-2 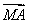 )=0,则△ABC为________三角形.
)=0,则△ABC为________三角形.
查看答案和解析>>
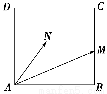
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用8练习卷(解析版) 题型:填空题
如图,在正方形ABCD中,已知AB=2,M为BC的中点,若N为正方形内(含边界)任意一点,则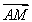 ·
·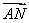 的最大值是________.
的最大值是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com