
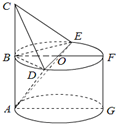
 (2012•肇庆二模)如图,AB是圆柱ABFG的母线,C是点A关于点B对称的点,O是圆柱上底面的圆心,BF过O点,DE是过O点的动直径,且AB=2,BF=2AB.
(2012•肇庆二模)如图,AB是圆柱ABFG的母线,C是点A关于点B对称的点,O是圆柱上底面的圆心,BF过O点,DE是过O点的动直径,且AB=2,BF=2AB.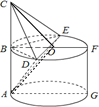 (1)证明:∵AB是圆柱ABFG的母线,C是点A关于点B对称的点,
(1)证明:∵AB是圆柱ABFG的母线,C是点A关于点B对称的点,| DE2-BD2 |
| 16-x2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 16-x2 |
x2+
| ||
| 4 |
| 16-x2 |
| 2 |
| 2 |
| BC |
| BO |
| 2 |
| 2 |
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
| π |
| 2 |


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案科目:高中数学 来源: 题型:
 (2012•肇庆二模)如图,某测量人员,为了测量西江北岸不能到达的两点A,B之间的距离,她在西江南岸找到一个点C,从C点可以观察到点A,B;找到一个点D,从D点可以观察到点A,C;找到一个点E,从E点可以观察到点B,C;并测量得到数据:∠ACD=90°,∠ADC=60°,∠ACB=15°,∠BCE=105°,∠CEB=45°,DC=CE=1(百米).
(2012•肇庆二模)如图,某测量人员,为了测量西江北岸不能到达的两点A,B之间的距离,她在西江南岸找到一个点C,从C点可以观察到点A,B;找到一个点D,从D点可以观察到点A,C;找到一个点E,从E点可以观察到点B,C;并测量得到数据:∠ACD=90°,∠ADC=60°,∠ACB=15°,∠BCE=105°,∠CEB=45°,DC=CE=1(百米).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com