
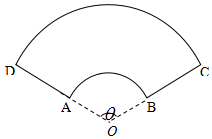
 某公司拟设计一个扇环形状的花坛(如图所示),该扇环是由以点O为圆心的两个同心圆弧和延长后通过点AD的两条线段围成.设圆弧$\widehat{AB}$、$\widehat{CD}$所在圆的半径分别为f(x)、R米,圆心角为θ(弧度).
某公司拟设计一个扇环形状的花坛(如图所示),该扇环是由以点O为圆心的两个同心圆弧和延长后通过点AD的两条线段围成.设圆弧$\widehat{AB}$、$\widehat{CD}$所在圆的半径分别为f(x)、R米,圆心角为θ(弧度).分析 (1)设花坛的面积为S平方米.$S=\frac{1}{2}{r_2}^2θ-\frac{1}{2}{r_1}^2θ$,即可得出结论;
(2)记r2-r1=x,则0<x<10,所以$S=\frac{1}{2}({\frac{40}{3}-\frac{4}{3}x})x$=$-\frac{2}{3}{({x-5})^2}+\frac{50}{3},x∈({0,10})$,即可得出结论.
解答 解:(1)设花坛的面积为S平方米.$S=\frac{1}{2}{r_2}^2θ-\frac{1}{2}{r_1}^2θ$…(2分)
=$\frac{1}{2}×36×\frac{π}{3}-\frac{1}{2}×9×\frac{π}{3}$=$\frac{9}{2}π({m^2})$…(4分)
答:花坛的面积为$\frac{9}{2}π({m^2})$;…(5分)
(2)$\widehat{AB}$的长为r1θ米,$\widehat{CD}$的长为r2θ米,线段AD的长为(r2-r1)米
由题意知60•2(r2-r1)+90(r1θ+r2θ)=1200
即4(r2-r1)+3(r2θ+r1θ)=40*…(7分)
$S=\frac{1}{2}{r_2}^2θ-\frac{1}{2}{r_1}^2θ=\frac{1}{2}({{r_2}θ+{r_1}θ})({{r_2}-{r_1}})$…(9分)
由*式知,${r_2}θ+{r_1}θ=\frac{40}{3}-\frac{4}{3}({{r_2}-{r_1}})$…(11分)
记r2-r1=x,则0<x<10
所以$S=\frac{1}{2}({\frac{40}{3}-\frac{4}{3}x})x$=$-\frac{2}{3}{({x-5})^2}+\frac{50}{3},x∈({0,10})$…(13分)
当x=5时,S取得最大值,即r2-r1=5时,花坛的面积最大.…(15分)
答:当线段AD的长为5米时,花坛的面积最大.…(16分)
点评 本题考查利用数学知识解决实际问题,考查扇形的面积,考查配方法的运用,属于中档题.


 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a2>b2 | B. | 2a>2b | C. | ${({\frac{1}{2}})^a}>{({\frac{1}{2}})^b}$ | D. | (a${\;}^{\frac{1}{2}}$>b${\;}^{\frac{1}{2}}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 4 | C. | 9 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 中学 | 甲 | 乙 | 丙 | 丁 |
| 人数 | 30 | 40 | 20 | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
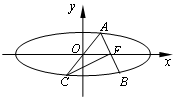 如图,椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的右焦点为F,过F的直线交椭圆于A,B两点,点C是点A关于原点O的对称点,若CF⊥AB且CF=AB,则椭圆的离心率为$\sqrt{6}-\sqrt{3}$.
如图,椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的右焦点为F,过F的直线交椭圆于A,B两点,点C是点A关于原点O的对称点,若CF⊥AB且CF=AB,则椭圆的离心率为$\sqrt{6}-\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | -$\frac{2}{3}$ | C. | $\frac{2\sqrt{2}}{3}$ | D. | -$\frac{2\sqrt{2}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{{2\sqrt{2}}}{9}$ | B. | $-\frac{{2\sqrt{2}}}{3}$ | C. | $-\frac{{4\sqrt{2}}}{9}$ | D. | $-\frac{4}{9}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com