
����Ŀ��Ϊ�����ļ����ºͶ�����ůʱ������Դ��ģ����ݵ��ݶ�����ǽ��Ҫ������Ȳ㣮ij��������Ҫ�����ʹ��20��ĸ��Ȳ㣬ÿ����ĸ��Ȳ㽨��ɱ�Ϊ6��Ԫ���ý�����ÿ�����Դ���ķ���C����λ����Ԫ������Ȳ���x����λ��cm�������ϵ��C��x��= ![]() ��0��x��10�������������Ȳ㣬ÿ����Դ���ķ���Ϊ8��Ԫ����f��x��Ϊ���Ȳ㽨�������20�����Դ���ķ���֮�ͣ�
��0��x��10�������������Ȳ㣬ÿ����Դ���ķ���Ϊ8��Ԫ����f��x��Ϊ���Ȳ㽨�������20�����Դ���ķ���֮�ͣ�
������k��ֵ��f��x���ı���ʽ��
�����Ȳ������ʱ���ܷ���f��x���ﵽ��С��������Сֵ��
���𰸡��⣺��������Ȳ���Ϊxcm�������裬ÿ����Դ���ķ���Ϊ ![]() ��
��
����C��0��=8����k=40����� ![]() ��
��
���������ΪC1��x��=6x�����ø��Ȳ㽨�������20�����Դ���ķ���֮��![]()
���� ![]() ����f'��x��=0����
����f'��x��=0���� ![]() ��
��
���x=5�� ![]() ����ȥ������0��x��5ʱ��f�䣨x����0����5��x��10ʱ��f�䣨x����0����x=5��f��x������Сֵ�㣬��Ӧ����СֵΪ
����ȥ������0��x��5ʱ��f�䣨x����0����5��x��10ʱ��f�䣨x����0����x=5��f��x������Сֵ�㣬��Ӧ����СֵΪ![]() ��
��
�����Ȳ���5cm��ʱ���ܷ��ôﵽ��СֵΪ70��Ԫ��
������������������ɵ�ÿ����Դ���ķ���Ϊ C ( x ) = ![]() ,�ָ���C��0��=8����k=40����� C ( x ) =
,�ָ���C��0��=8����k=40����� C ( x ) =![]() ���������ΪC1��x��=6x�����ø��Ȳ㽨�������20�����Դ���ķ���֮�� f ( x ) = 20 C ( x ) + C1 ( x ) = 20 ��
���������ΪC1��x��=6x�����ø��Ȳ㽨�������20�����Դ���ķ���֮�� f ( x ) = 20 C ( x ) + C1 ( x ) = 20 �� ![]() + 6 x =
+ 6 x = ![]() + 6 x ( 0 �� x �� 10��
+ 6 x ( 0 �� x �� 10��
������������ֵ��f'��x��=0��![]() ���x=5�� x =
���x=5�� x = ![]() ����ȥ��.��0��x��5ʱ��f�䣨x����0����5��x��10ʱ��f�䣨x����0����x=5��f��x������Сֵ�㣬��Ӧ����СֵΪ f ( 5 ) = 6 �� 5 +
����ȥ��.��0��x��5ʱ��f�䣨x����0����5��x��10ʱ��f�䣨x����0����x=5��f��x������Сֵ�㣬��Ӧ����СֵΪ f ( 5 ) = 6 �� 5 + ![]() = 70 �������Ȳ���5cm��ʱ���ܷ��ôﵽ��СֵΪ70��Ԫ
= 70 �������Ȳ���5cm��ʱ���ܷ��ôﵽ��СֵΪ70��Ԫ



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��A��0����2������ԲE�� ![]() +
+ ![]() =1��a��0��b��0����������Ϊ
=1��a��0��b��0����������Ϊ ![]() ��F����ԲE���ҽ��㣬ֱ��AF��б��Ϊ
��F����ԲE���ҽ��㣬ֱ��AF��б��Ϊ ![]() ��O������ԭ�㣮
��O������ԭ�㣮
��1����E�ķ��̣�
��2�������A��ֱ��l��E�ཻ��P��Q���㣬����OPQ��������ʱ����ֱ��l�ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڵȲ�����{an}�У�a2+a7=��23��a3+a8=��29�� ����������{an}��ͨ�ʽ��
����������{an+bn}������Ϊ1������Ϊc�ĵȱ����У���{bn}��ǰn���Sn ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������д���ĸ���Ϊ���� ��
��y= ![]() ��ͼ����ڣ�0��0���Գƣ�
��ͼ����ڣ�0��0���Գƣ�
��y=x3+x+1��ͼ����ڣ�0��1���Գƣ�
��y= ![]() ��ͼ�����ֱ��x=0�Գƣ�
��ͼ�����ֱ��x=0�Գƣ�
��y=sinx+cosx��ͼ�����ֱ��x= ![]() �Գƣ�
�Գƣ�
A.0
B.1
C.2
D.3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ŷ����ʦ���ø�ʱ��ͬѧ����һ����ѧ��ҵ����ͬһ��ֱ������ϵ�л����ĸ�����������ͼ��ʹ���ǵĵ����ֱ�Ϊ ![]() ��
�� ![]() ��ʱ��ͬѧΪ�˺�ĺ��ͬѧ��ȥ�棬�ʴ�Ӣͬѧ������ҵ���ܿ�ͳ����ˣ������ͼ���ڶ��죬ŷ����ʦ��������ʱ��ͬѧ�����㻭�����������У������ǵ���Ϊe�Ķ�������ͼ��ʱ��ͬѧ�����Զԣ��������ͨ�죬�ۿ�ʱ��ͬѧ��Ҫ��ŷ����ʦѵ��һ����������ǵ����ܲ��ܰ���һ�ѣ��ش���������أ��������ǵ���Ϊe�Ķ���������ͼ��
��ʱ��ͬѧΪ�˺�ĺ��ͬѧ��ȥ�棬�ʴ�Ӣͬѧ������ҵ���ܿ�ͳ����ˣ������ͼ���ڶ��죬ŷ����ʦ��������ʱ��ͬѧ�����㻭�����������У������ǵ���Ϊe�Ķ�������ͼ��ʱ��ͬѧ�����Զԣ��������ͨ�죬�ۿ�ʱ��ͬѧ��Ҫ��ŷ����ʦѵ��һ����������ǵ����ܲ��ܰ���һ�ѣ��ش���������أ��������ǵ���Ϊe�Ķ���������ͼ��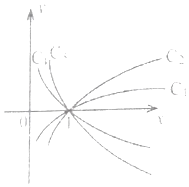
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��f��x���Ƕ�����R�ϵ�ż������������x��R������f��x��=f��x+4�����ҵ�x��[��2��0]ʱ��f��x��=�� ![]() ��x��1���������䣨��2��6]�ڹ���x�ķ���f��x����loga��x+2��=0��a��1��ǡ��������ͬ��ʵ��������a��ȡֵ��Χ�ǣ� ��
��x��1���������䣨��2��6]�ڹ���x�ķ���f��x����loga��x+2��=0��a��1��ǡ��������ͬ��ʵ��������a��ȡֵ��Χ�ǣ� ��
A.�� ![]() ��2��
��2��
B.�� ![]() ��2��
��2��
C.[ ![]() ��2��
��2��
D.�� ![]() ��2]
��2]
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���ʣ�0�� ![]() �����¡ʣ�0��
�����¡ʣ�0�� ![]() ����������
���������� ![]() cos2
cos2 ![]() +
+ ![]() sin2
sin2 ![]() =
= ![]() +
+ ![]() ��sin��2017������=
��sin��2017������= ![]() cos��
cos�� ![]() �Щ��£������+��= ��
�Щ��£������+��= ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���� ![]() ��
�� ![]() ��
��
������ ![]() ��
�� ![]() ���ߣ���x��ֵ��
���ߣ���x��ֵ��
������ ![]() ��
�� ![]() ����x��ֵ��
����x��ֵ��
����x=2ʱ���� ![]() ��
�� ![]() �нǦȵ�����ֵ��
�нǦȵ�����ֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com