
【题目】某小组6个人排队照相留念.
(1)若分成一排照相,有多少种不同的排法?
(2)若排成一排照相,甲、乙两人必须在一起,有多少种不同的排法?
(3)若排成一排照相,其中甲必在乙的右边,有多少种不同的排法?
(4)若排成一排照相,其中有3名男生3名女生,且男生不能相邻有多少种排法?
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]() (4)
(4)![]()
【解析】
(1)6人的全排列,即可得出答案;
(2)由“捆绑法”结合分步乘法计数原理求解即可;
(3)由甲在乙的右边与甲在乙的左边的排法各占一半,即可得出答案;
(4)先排女生,采用插空法得出男生的排法,结合分步乘法计数原理,即可得出答案.
(1)6人排成一排照相,即为6人的全排列,即有![]() 种不同的排法.
种不同的排法.
(2)采用“捆绑法”,即甲、乙两人看成一个人,这样有![]() 种不同的排法,然后甲、乙两人之间再排队,有
种不同的排法,然后甲、乙两人之间再排队,有![]() 种排法,由分步乘法计数原理得出有
种排法,由分步乘法计数原理得出有![]() 种排法.
种排法.
(3)甲在乙的右边与甲在乙的左边的排法各占一半,所以有![]() 种排法.
种排法.
(4)先排女生,有![]() 种排法,再把3个男生插入这3个女生形成的空档中(包括两端),这样男生有
种排法,再把3个男生插入这3个女生形成的空档中(包括两端),这样男生有![]() 种排法,由分步乘法计数原理可知有
种排法,由分步乘法计数原理可知有![]() 种排法.
种排法.


科目:高中数学 来源: 题型:
【题目】某媒体为调查喜爱娱乐节目![]() 是否与观众性别有关,随机抽取了30名男性和30名女性观众,抽查结果用等高条形图表示如图:
是否与观众性别有关,随机抽取了30名男性和30名女性观众,抽查结果用等高条形图表示如图:
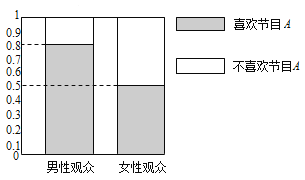
(1)根据该等高条形图,完成下列![]() 列联表,并用独立性检验的方法分析,能否在犯错误的概率不超过0.05的前提下认为喜欢娱乐节目
列联表,并用独立性检验的方法分析,能否在犯错误的概率不超过0.05的前提下认为喜欢娱乐节目![]() 与观众性别有关?
与观众性别有关?

(2)从性观众中按喜欢节目![]() 与否,用分层抽样的方法抽取5名做进一步调查.从这5名中任选2名,求恰有1名喜欢节目
与否,用分层抽样的方法抽取5名做进一步调查.从这5名中任选2名,求恰有1名喜欢节目![]() 和1名不喜欢节目
和1名不喜欢节目![]() 的概率.
的概率.
附:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
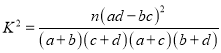 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,AB//CD,且![]() .
.

(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC, ![]() ,求二面角A-PB-C的余弦值.
,求二面角A-PB-C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱锥S-ABC的底面是以AB为斜边的等腰直角三角形,SA=SB= SC=2,AB=2,设S、A、B、C四点均在以O为球心的某个球面上。则点O到平面ABC的距离为________________。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某单位有甲、乙、丙三个部门,从员工中抽取7人,进行睡眠时间的调查.若抽出的7人中有4人睡眠不足,3人睡眠充足,现从这7人中随机抽取3人做进一步的身体检查.
(1)用X表示抽取的3人中睡眠不足的员工人数,求随机变量X的分布列与数学期望;
(2)设A为事件“抽取的3人中,既有睡眠充足的员工,也有睡眠不足的员工”,求事件A发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】调查某校高三年级男生的身高,随机抽取40名高三男生,实测身高数据(单位:cm)如下:
171 | 163 | 163 | 166 | 166 | 168 | 168 | 160 | 168 | 165 |
171 | 169 | 167 | 169 | 151 | 168 | 170 | 168 | 160 | 174 |
165 | 168 | 174 | 159 | 167 | 156 | 157 | 164 | 169 | 180 |
176 | 157 | 162 | 161 | 158 | 164 | 163 | 163 | 167 | 161 |
(1)作出频率分布表;
(2)画出频率分布直方图.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆周上分布着2002 个点,现将它们任意地染成白色或黑色,如果从某一点开始,依任一方向绕圆周运动到任一点,所经过的(包括该点本身)白点总数恒大于黑点总数,则称该点为好点.为确保圆周上至少有一个好点,试求所染黑点数目的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com