
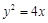 ,直线l过定点
,直线l过定点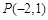 ,斜率为k.当k为何值时,直线l与该抛物线:只有一个公共点;有两个公共点;没有公共点?
,斜率为k.当k为何值时,直线l与该抛物线:只有一个公共点;有两个公共点;没有公共点?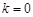 ,
, 或
或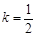 ,此时直线l与该抛物线只有一个公共点;当
,此时直线l与该抛物线只有一个公共点;当 ,此时直线l与该抛物线有两个公共点;当
,此时直线l与该抛物线有两个公共点;当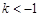 或
或 ,此时直线l与该抛物线没有公共点.
,此时直线l与该抛物线没有公共点.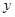 的一元二次方程,利用判别式的符号判定直线与抛物线的交点个数.规律总结:解决直线与圆锥曲线的交点个数,一般思路是联立直线与圆锥曲线的方程,整理得到关于
的一元二次方程,利用判别式的符号判定直线与抛物线的交点个数.规律总结:解决直线与圆锥曲线的交点个数,一般思路是联立直线与圆锥曲线的方程,整理得到关于 或
或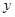 的一元二次方程,利用判别式的符号进行判定.注意点:当整理得到的一元二次方程的二次项系数为字母时,要注意讨论二次项系数是否为0.
的一元二次方程,利用判别式的符号进行判定.注意点:当整理得到的一元二次方程的二次项系数为字母时,要注意讨论二次项系数是否为0.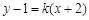 ,
,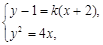 得
得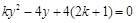 .
.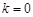 时,知方程有一个解,直线l与该抛物线只有一个公共点.
时,知方程有一个解,直线l与该抛物线只有一个公共点.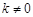 时,方程的判别式为
时,方程的判别式为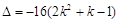 ,
,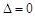 ,则
,则 或
或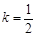 ,此时直线l与该抛物线只有一个公共点.
,此时直线l与该抛物线只有一个公共点.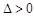 ,则
,则 ,此时直线l与该抛物线有两个公共点.
,此时直线l与该抛物线有两个公共点.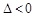 ,则
,则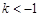 或
或 ,此时直线l与该抛物线没有公共点.
,此时直线l与该抛物线没有公共点.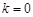 ,
, 或
或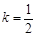 ,此时直线l与该抛物线只有一个公共点;
,此时直线l与该抛物线只有一个公共点; ,此时直线l与该抛物线有两个公共点;
,此时直线l与该抛物线有两个公共点;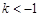 或
或 ,此时直线l与该抛物线没有公共点.
,此时直线l与该抛物线没有公共点.

 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源:不详 题型:单选题
| x2 |
| a2 |
| y2 |
| b2 |
| PM |
| PN |
A.
| B.
| C.
| D.
|
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| y2 |
| 25 |
| x2 |
| 9 |
| y2 |
| 25 |
| x2 |
| 9 |
| y2 |
| 25 |
| x2 |
| 9 |
| 3 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.双曲线 | B.双曲线左边一支 |
| C.一条射线 | D.双曲线右边一支 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com