
| A. | (-4,+∞) | B. | (-∞,-1)∪(3,+∞) | C. | (-∞,-1]∪[3,+∞) | D. | (-4,-1]∪[3,+∞) |
分析 由对任意的实数x1,x2(x1≠x2)都有$\frac{{f({x_1})-f({x_2})}}{{{x_1}-{x_2}}}$<0,可得f(x)在R上递减,由分段函数可得$\left\{\begin{array}{l}{-(m+4)<0}\\{m≤{m}^{2}-m-3}\end{array}\right.$,解不等式即可得到所求m的范围.
解答 解:由对任意的实数x1,x2(x1≠x2)都有$\frac{{f({x_1})-f({x_2})}}{{{x_1}-{x_2}}}$<0,可得
f(x)在R上递减,
由函数f(x)=$\left\{\begin{array}{l}-x+m\\-(m+4)x+{m^2}-m-3\end{array}$$\begin{array}{l},x≥0\\;x<0\end{array}$,可得
$\left\{\begin{array}{l}{-(m+4)<0}\\{m≤{m}^{2}-m-3}\end{array}\right.$即为$\left\{\begin{array}{l}{m>-4}\\{m≥3或m≤-1}\end{array}\right.$,
解得m≥3或-4<m≤-1.
故选:D.
点评 本题考查函数单调性的性质及其应用,理解“对任意的实数x1≠x2,都有$\frac{{f({x_1})-f({x_2})}}{{{x_1}-{x_2}}}$<0成立?函数f(x)在定义域内单调递减”是关键,也是难点所在,考查解不等式组的能力,属于中档题.


科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
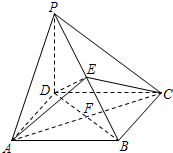 如图,在四棱锥P-ABCD中,PD⊥平面ABCD;四边形ABCD是菱形,经过AC作与PD平行的平面交PB与点E,ABCD的两对角线交点为F.求证:AC⊥DE.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD;四边形ABCD是菱形,经过AC作与PD平行的平面交PB与点E,ABCD的两对角线交点为F.求证:AC⊥DE.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com